In this post
When we combine two different expressions and show them as equal to one another, we have an equation. An easy way to remember this is that the equation contains an equals sign.
Solving equations
When it comes to finding out an unknown value that is in an equation, we must try to isolate the term and then use the others to find its value.
Key term
Isolating terms
The method of taking a term and moving it to one side of an equation to be on its own.
Example
I have 4 eggs, how many more do I need to get a dozen?
Since a dozen is 12, this can be converted to the equation:
Where we must find the value of x. To do this we can change the other terms in the equation, so if we minus 4 from each side we get:
We can check our answer of 8 by putting it back into the equation we started with, by replacing x with 8, we get 
which is clearly correct so we must have the right answer.
Rules of solving
There are certain rules that we must obey when solving equations. The main one being that what we do to one side of the equation must be done to the other also. This is similar to when we worked with fractions and we had to do the same to the top and bottom of any fraction.
When we talk of the ‘sides’ of an equation this means the different sides of the equals sign. So in the equation , one side is 
and the other is 12.
If we were to add, subtract or do any other operations to one side, we must do exactly the same to the other to make sure that the equation is always equivalent to the original. This can be thought of as having the equation as weighing scales with the equals in the middle, and the scales must always be level. Therefore, if we add weight to one side, we must add the same amount to the other so the scales are still balanced.
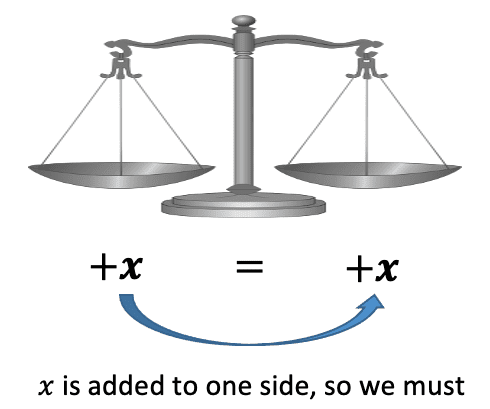
Isolating terms
When we have an unknown in an equation, we may be asked to ‘solve for the unknown’. To do this we must ‘isolate’ the unknown term by getting it onto one side of the equation on its own. To do this we need to move the other values that are on the same side as the unknown term.
We simply must do the operation that would make the value disappear on one side, but we must also remember to do the same to the other side of the equation. For example:
Here we must isolate the term, therefore we need to move the 7. To get the y on its own, we must minus off the value of 7 to make it disappear, however, we must then also do this to the other side.
This gives us an answer of 74 for y. Since the positive and negative 7 on the left side of the equation cancel each other to give 0. So we are left with just y on this side (it has been ‘isolated’ to be on its own).
An alternative method
A different way of solving equations which some people prefer is to literally ‘move’ different terms from one side to the other. However, when doing this we must remember that when a term moves from one side of an equation to the other, it must become its opposite. So, if we were to move a positive term, it would become negative on the opposite side. And if we moved a multiplication, it would become a division and vice versa.
becomes
becomes
becomes 
becomes
This method is essentially the same as the first and would give the exact same answer when done correctly. For example:
Here we must move the 7 from the left to the right:
When the 7 is moved, as soon as it crosses the equals sign, it disappears from the left, becomes 
instead and is put on the right. Therefore, we get:
Clearly this gives exactly the same answer but can save time, and some students prefer this method. Either one is perfectly valid to use.
Example
Isolate the term x:
| Using the first method | Using the alternative method |
|---|---|
First, we must minus 13 from both sides to get This cancels the 13 from the left, and the right can be calculated to get Now we must get rid of the 2 on the left which is multiplied by x. To do this we need to divide by 2, however, we must also do this to the other side of the equation so that it is still balanced. This gives  So is equal to 7. | Here we need to move the +13 which will become –13 once it crosses the equals sign. This gives Which is equal toNow we have a 2 that is multiplied; moving this it will become a division on the other side Which gives the answer asSo is equal to 7. |
The above equation has two different operations that are done to the unknown x. So you may be wondering why we did the subtraction of 13 before the multiplication of 2. This is because when there is more than one operation, we must use BIDMAS (as seen in earlier lessons), but this time we use it in reverse!
So we must first deal with the subtraction, then addition and so on, ending with any brackets that may be in the equation.
Example
Write out the order of operations to solve for x:
a) 
b) 
a) In the first of these we have a multiplication and subtraction. When using the reverse of BIDMAS, we deal with the subtraction first and then the multiplication. Therefore, we must add 98 to both sides and then divide by 5.
b) Here we have an indices and a division that are operating on the unknown x. Again, following the reverse of BIDMAS we must do the division first and then the indices. So we multiply both sides by 6, then find the square root of both.
Double check
Checking your answer is very quick to do with equations and unknowns. For this reason it is recommended that you do it with all answers to avoid any mistakes. Steps for checking:
1) Substitute the value for the unknown into the left-hand side of the original equation and work out what it is equal to. into the original gives us 
which is 27.
2) Substitute unknowns into the right-hand side of the original equation. In our example the right does not have any unknowns and is simply equal to 27, however, this may not always be the case.
3) Check that the left- and right-hand side are the same number. So we got 
for the left and the right as 27. Clearly 
so we have the correct answer.
Negative unknowns
In the above activity you may have noticed that the last few questions had an unknown which was a negative. If you managed to figured out how to solve these then well done!
When we have an unknown which is a negative we can simply recognise that this is the same as multiplying by negative 1.
Therefore 
and the equation can be solved by simply treating this as another operation on x. To undo this we must multiply by 
as this would then make 
equal to just 
. So this is how we get rid of a negative unknown. Of course, for this to work we must also follow the rule of doing the same to the other side, therefore both sides are multiplied by .
Example
Solve 
for x.
First we need to minus 7 from both sides to get 
and now we can simply replace this with 
and notice that to remove the minus 1 we need to multiply by and this must be done to both sides. Giving us 
which is equal to 
. So x is equal to -3.
Unknown values on both sides of an equation
When we find an unknown value on both sides of an equation a little more work is needed to get to a solution. We must move one side to the other giving us a new value for the unknown on only one side. This is the same as doing an operation on both sides.
Example
Solve for the equation 
Here we have 
on one side of the equation and 
on the other. Therefore, we should try to use the and take this away from both sides. All the rules of equations we have already seen still apply to this term, and subtracting this amount is the same as ‘moving’ it to the other side if you prefer this method. So we get:
This can then be solved exactly the same as examples we have already seen to find that 
.
It does not matter if we were to minus from both sides or as either of these operations would result in there being unknowns only on one side. However, we choose to minus as this avoids us getting an equation that has a negative unknown value, however, we have already discussed how to solve these and this would result in the same answer.
Example
Solve 
for x
Here we must first multiply out the brackets before we move terms. This becomes:
Minus 
from both sides:
Now we must subtract 14 from both sides and then divide by 5 to fully isolate the x term.
Further techniques
Two more techniques that we can use are to help us solve equations with square numbers and fractions. First we will look at squares:
If we ‘square’ a number then the inverse of this is to ‘square root’ since these two operations cancel each other. This knowledge can be used when solving equations where the unknown value is either squared or square rooted. We can simply do the inverse (still to both sides of the equation) to isolate the unknown term.
Example
Solve for :
a) 
b) 
c) 
a) Here we have 
which we need to change to just x, therefore we must do the square root of both sides of the equation. This gives us 
which equals
b) Here we must first move the 
to the other side (using the inverse of the BIDMAS rule) to give 
and now we need the inverse of a square root so we must square both sides of the equation. Giving 
which is the same as 
c) Here we need to take the inverse of the square root first because 
is inside the square root symbol. Therefore, we can think of there being a bracket around 
so we must do this bit last. Squaring both sides gives 
which is easily solved to get 
.
Another technique that we can use when solving equations is put into practice when we have an unknown value on the bottom of a fraction. When this happens we can ‘swap’ the value at the bottom with the other side of the equation.
Example
Solve for 
the equation 
Since we have the unknown on the left-hand side of this equation and on the bottom of the fraction, it can be swapped with the right-hand side value. This gives us a new equation of 
which can easily be solved for 
.
This rule is better understood if we look at the rule with no unknowns and just normal numbers. For example, the equation 
is correct, however, so is the equation 
where the bottom of the fraction and the opposing side are swapped. Therefore, this rule does not make the equation untrue.
Example
Find the value of in:
a) 
b) 
c) 
a) By swapping the value on the bottom with the value on the right we get 
so 
b) Doing the same again but this time moving the entire bottom of the fraction so all of 
moves to the right of the equation. This gives us 
which means 
so
c) Using the same method as part (b) we get 
which is the same as 
. This is then solved using techniques we have already learnt in the lesson to find 
