If a diameter of a circle is at a right angle to a chord then it splits the chord into two equal parts. This can be of use when we have a diameter line (which must pass through the centre of the circle) that intersects a chord drawn in. If the angle made by the two lines is at 
then the diameter will split the chord into two equal sections.
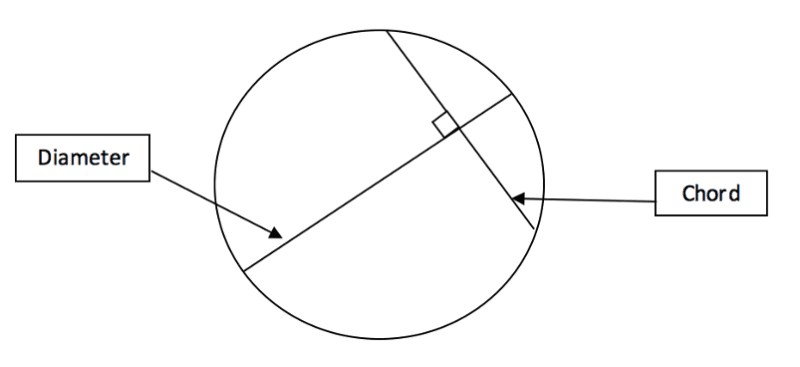
We can also swap this definition to say that if a chord passes through a line in the circle at then that line must pass through the centre of the circle. As well as this the two triangles that can be made by connecting the end of the chord line to the end of the diameter line will be identical. This is shown below.
Example
The point O below is at the centre of the circle. Find the length of BC if OC is 5cm and the radius of the circle is 7.5cm. Leave your answer to 2dp.
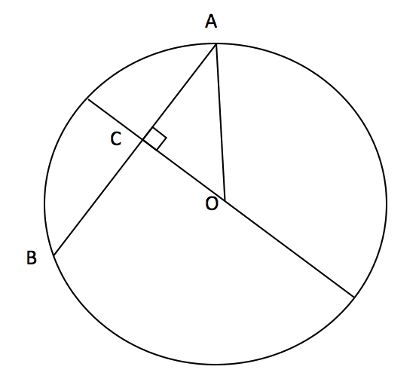
Here we can first find the length of AC since we have a right-angled triangle with hypotenuse 7.5cm (AO) and another side 5cm (OC). This gives a value for the length of AC using Pythagoras: 
so 
so 
to 2dp. However, we were asked to find BC but since this must be equal to AC, since AB is a chord at 90° to the diameter line, then 
.
Clearly, we must treat each problem individually and look for ways to calculate the different lengths which may then help us to find the one which we are actually searching for. The use of other techniques such as Pythagoras’ theorem will always come in handy, and whenever you see a right angle you should be ready to use this theory.
