In this post
What is trigonometry?
Trigonometry is a very powerful technique in mathematics and deals with the sides and angles of triangles. Unlike Pythagoras, which only gives relations between the sides of right-angled triangles, trigonometry will help us to relate the sides AND angles in triangles.
The way in which trigonometry works is because of similarities between triangles and the fact that, since one angle must be 
, we can use the others and relate these to the side lengths through similar triangles. If we look at some similar right-angled triangles below and form a ratio of the different angles we will be able to see how trigonometry is used.
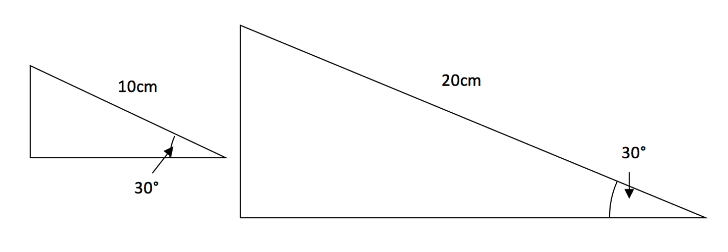
If we form a ratio of the hypotenuse and other known sides of these two triangles we get 
but if we now get out our calculators and type in we will see that this gives us the answer of 
also. Therefore, we can use the sin function on a calculator to help us work out angles and side lengths. Any triangle that is similar to the ones shown above will use the same ratio, so we could essentially find the side lengths and angles for any triangle, of any size, as long as it is similar to the above.
We can now look to broaden this rule into something that we can use for any sized right-angled triangle.
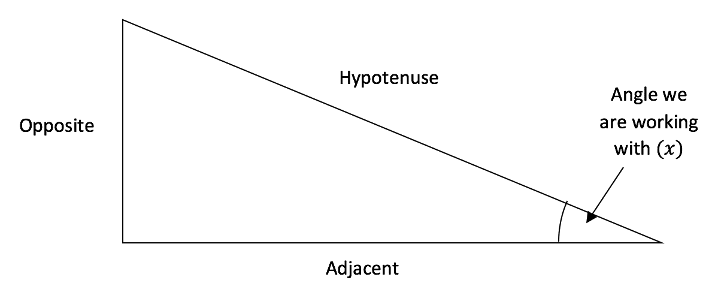
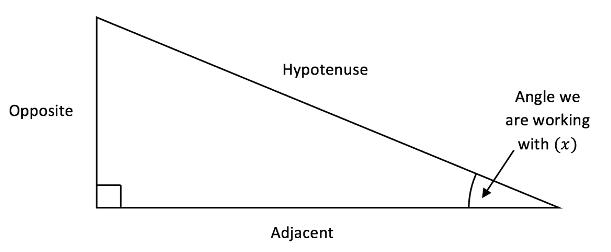
Here we have labelled the different sides of the triangle as hypotenuse, opposite and adjacent. The hypotenuse is always the longest side of the triangle that is across from the 
angle, but the other two sides can be swapped and depend on which angle we are working with. The opposite side is the one that is directly across from the angle that we are looking at and the adjacent is the remaining side next to the angle in question.
The rule shown above can be used for any right-angled triangle to help us find unknown side lengths when we rearrange. However, before we can do this we need to be able to recognise and label the correct sides of a triangle for any particular problem.
The Sine ratio
Before we had the ratio of 
which we can then make more generic if we label the sides of a triangle as above. We get the rule that:
Where x is the angle that we are looking at and is in degrees. This is obviously a very useful formula and can be used for any sized right-angled triangle to help us work out the side lengths. If we have the known angle and either the opposite or hypotenuse then we can rearrange this formula to tell us the length of the remaining side.
Example
Given a right-angled triangle with an angle of 
and a hypotenuse of 10cm, find the opposite side length.
By putting the values given into the formula we get 
and we can find the value of 
using our calculator as 0.57 (2dp). So, when rearranging the formula we get 
giving us a value for the Opposite = 5.7cm.
Example
Find the hypotenuse of the triangle below.
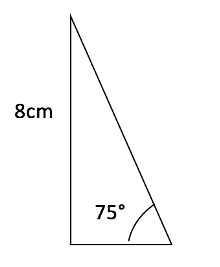
Again, using the sine formula we get 
which, when working out the value of 
as 0.97 (2dp) and rearranging gives us a value of the hypotenuse as 8.25cm.
Cosine and Tangent
There are also uses for cosine and tangent when it comes to right-angled triangles and these both work in a very similar way to the use of sine which we have already seen. Again, they both give us formulae for working outside lengths and angles. The only difference is their respected formulas. These are shown below for both cosine and tangent.
As in the earlier part of this lesson, the meaning of hypotenuse is always the longest edge that is across from the 90° angle and the opposite and adjacent angles are again related to which angle we are working with.
When working with these new formulas, we must set the problem out in the same way as before and try to use the angles and sides that we already know to find the values of any unknowns in the triangle. Depending on which side lengths we know, we use different formulas to enable us to work out any unknowns. This is for obvious reasons, as we will need to tailor each formula to the specific triangle in the question.
A trick to getting the right trigonometry formula
One of the best ways to identify which of the three formulas that we have seen is to label all of the sides of the triangle as hypotenuse, opposite and adjacent. Then we can see which of the three we already know. Next, we can simply use the technique known as:
SohCahToa
This word ‘sohcahtoa’ relates to which of the angles we know and what the correct formula is.
| Soh | Cah | Toa |
|---|---|---|
 |  |  |
From ‘SohCahToa’ we can use the letters S, C and T to refer to sin, cos or tan and the other letter to find the correct ratio between the opposite, adjacent and hypotenuse sides. Then we will know which of the three equations to use depending on what parts of the triangle we already know.
Steps for using trigonometry to identify unknown sides
1) Find the angle that we are working with.
2) Label the different sides hypotenuse, opposite and adjacent. Remember that the hypotenuse is always the same but the opposite and adjacent depend on which angle we are looking at.
3) Use SohCahToa to decide which of the three formulae we need to use for the wanted angle; the unknown angle and the one that is known will be used.
4) Put the correct numbers into the formula and rearrange for the unknown side.
Using a calculator with trigonometry
Clearly, when we are using trigonometry we must use the correct buttons on our calculator which we may not have used before. It is very easy to use and each of ‘sin’, ‘cos’ and ‘tan’ have their own buttons and we simply use these and then type in the correct angle.
It is advised that you practise the use of the different trigonometric functions on your calculator.
Inverting trigonometric functions
In order to find unknown angles of a right-angled triangle we can use the exact same formulae and rules for finding them as we have already seen in this lesson. However, as you will see, when we put the known values into a formula we are left with the unknown angle within a trigonometric function, such as below.
To find the unknown angle x we must rearrange the formula by taking the inverse of the function sin. This will then leave us with just the angle under investigation on one side and an inverse sin function on the other.
This can then be used with the inverse sin function on a calculator to give us the answer for the unknown angle. Here we must be very careful to use the inverse trig function instead of the normal one and to check the answer when it is found to avoid any mistakes.
Example
Find the unknown angle in the right-angled triangle below.
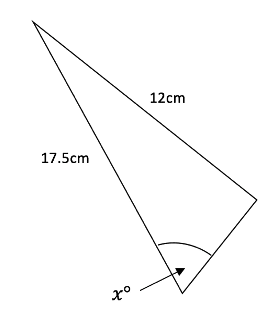
Here we have the side lengths which correspond to the opposite and hypotenuse sides. Therefore, from SohCahToa, we can tell we need the formula
Which when plugging in and rearranging for the unknown gives us the answer 
