In this post
Finding the area of a circle sector
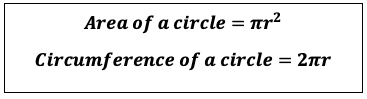
To find the space taken up by a circle sector we just need to recognise that the sector will be a certain percentage of the entire circle. Therefore, by finding the angle of the sector we can easily find out how much of the full circle the sector is and then use the area of the entire circle to find the area of the smaller sector.
So the area of the sector shown below, with an angle ![]() , must be proportional to the entire area of the circle. Since, instead of the full
, must be proportional to the entire area of the circle. Since, instead of the full ![]() we only have
we only have ![]() this will be seen in the difference of the areas between the full circle and sector.
this will be seen in the difference of the areas between the full circle and sector.
So the formula for a circle sector of x degrees is:

Finding the length of an arc
The same reasoning that we have just used can be applied to finding the length of an arc on a particular circle. By realising that the arc length is going to be a percentage of the entire circumference then we can easily see that the arc length with angle x is equal to:

This is just a proportion of the entire perimeter of the circle: which is all an arc is. So for the circle below with radius 5cm, arc of length AB and an angle of ![]() we can find the arc length:
we can find the arc length:
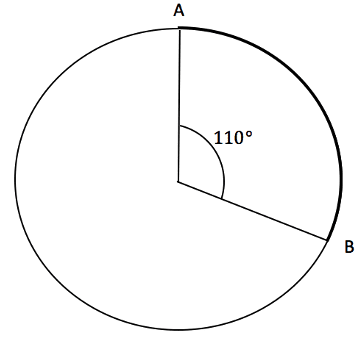
The above therefore gives us a value for the arc AB as:

Example
Find the area of the shaded part of this circle which has radius 11cm if the angle x is equal to ![]() :
:
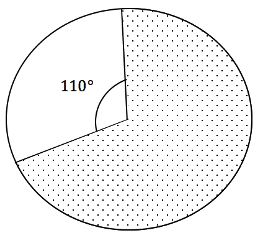
Since the angle x is equal to ![]() then the angle of the part which is shaded must be equal to
then the angle of the part which is shaded must be equal to ![]() and has a radius of 11cm. Therefore we can easily put the values into the equation:
and has a radius of 11cm. Therefore we can easily put the values into the equation:

Example
The area of a circle sector is ![]() and it is
and it is ![]() of the full circle. What is the radius of this circle?
of the full circle. What is the radius of this circle?
Here we are told the area of the sector but we must then find the radius. We are told that the sector is ![]() Taking our equation and then putting in the values that we are told gives us:
Taking our equation and then putting in the values that we are told gives us:

Rearranging for the value r gives: