The Doppler effect

August 17, 2022

In this post

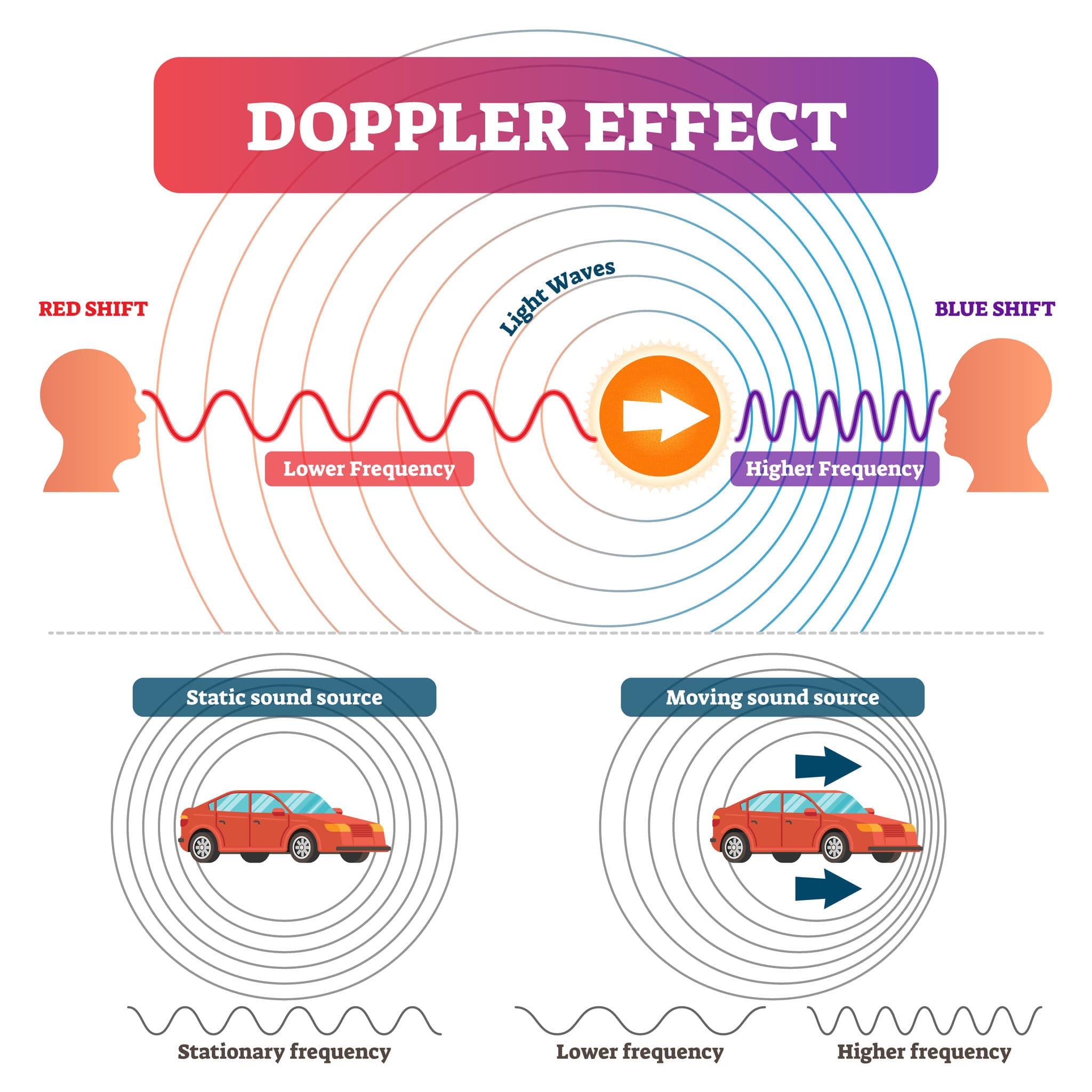
When a wave source is moving relative to an observer, there will be a change in the observed frequency and wavelength. This is known as the Doppler effect, and a good example which demonstrates this is the change in the sound of an ambulance’s siren as it approaches and moves past you.

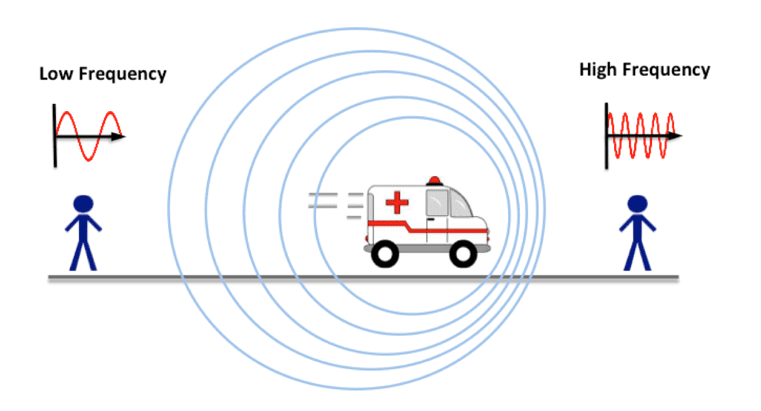
As shown in the diagram, as the ambulance travels towards you the frequency of the waves is increased and the sound will be higher in pitch. Once the ambulance has passed you and is travelling away, the frequency of the waves decreases and the sound is lower in pitch.

The Doppler effect is also observed with light waves. When a source of light is travelling towards you, the light waves will be closer together with a shorter wavelength and higher frequency. When the source of light is moving away from you, the light waves will be stretched out with a longer wavelength and lower frequency. Red light has a long wavelength and lower frequency, whereas the light at the blue/violet end of the visible spectrum has a shorter wavelength and higher frequency.

Red-shift

A spectrum shows the seven colours making up visible light. A spectroscope can be used to view the absorption spectrum for any light emitting object. Dark lines would be seen in the spectrum where light at that frequency and wavelength has been absorbed.

If we looked at the absorption spectrum for light on Earth emitted by our closest star, the Sun, we would observe dark lines in specific positions. If we then compared this to an absorption spectrum produced using light from a star which is the same size as the Sun in another galaxy, we would see that the position of the dark lines would shift towards the red end of the spectrum as shown in the diagram below.

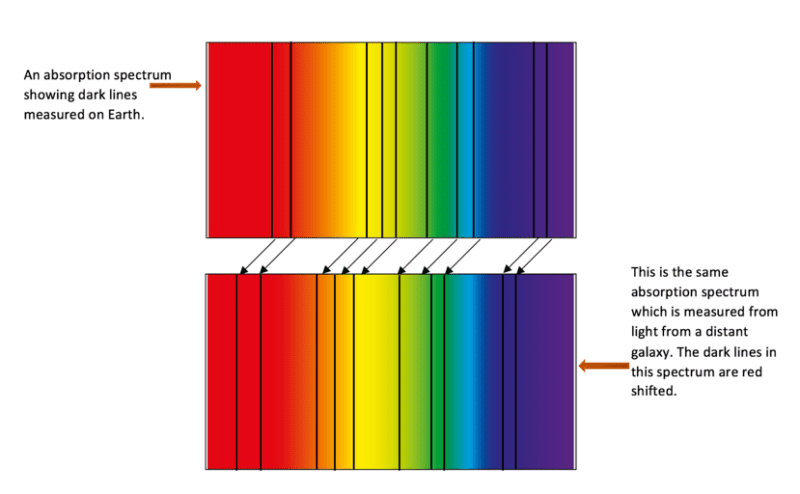
This shift towards the red end of the spectrum is the effect known as red-shift. It occurs because the galaxy is moving away from us and we are moving away from it. The distance between us is increasing which means that the wavelength of light also increases. The red end of the spectrum is where the light with the longest wavelengths is found, so the more the wavelength increases, the further over to the right the light emitted will be.

This red-shift is due to the fact that the light source is moving away from us and we are moving away from it at the same time. This shows that the universe is expanding and is used as the second piece of evidence for the Big Bang theory. The greater the red-shift, the further and faster the star is moving away from us. Stars in galaxies which are further away from ours produce a greater red-shift in light, which also shows that the galaxies are moving faster the further they are away from us.

If a galaxy was spinning, the light emitted would show both a red-shift and a blue-shift as the two edges of the galaxy moved further away from Earth and back towards the Earth. The main evidence that supports the Big Bang theory is summarised in the table below:

Evidence	Interpretation
Light from other galaxies is red-shifted.	The galaxies are moving away from us.
The further a galaxy is from us, the more it is red-shifted.	The whole universe is expanding from one single explanation.
The cosmic microwave background exists.	The uniform background radiation is energy remaining from the Big Bang.

Calculating the speed of a galaxy

The red-shift of light can be used to calculate the speed at which a galaxy is moving away from us. The equation that relates the changes in wavelength that occur during red-shift to the velocity of a galaxy and speed of light is:

\[ \frac{\text{change in wavelength}}{\text{reference wavelength}} = \frac{\text{velocity of a galaxy}}{\text{speed of light}} \]

\[ \frac{\lambda - \lambda_0}{\lambda_0} = \frac{\Delta \lambda}{\Delta_0} = \frac{v}{c} \]

This equation shows us that the change in the wavelength divided by the usual wavelength is equal to the velocity of the galaxy over the speed of light. Since the speed of light is constant, we can find the speed at which a galaxy is travelling as long as we have the reference wavelength and the measured wavelength for the light emitted.

Example

The absorption lines of hydrogen are measured at a wavelength of 656.285 nm in a laboratory. The same absorption lines are measured at a wavelength of 656.943 nm for a star in a nearby galaxy. Calculate the galaxy’s speed and deduce the direction in which it is travelling. We know that the speed of light is constant at 3 x 10⁸ m/s, and the wavelength measured in the laboratory is our reference wavelength λ_0.

The change in wavelength (Δ λ) is calculated by subtracting the reference wavelength from the measured wavelength (λ): 656.943 – 656.285 = 0.658.

Substituting these values into the equation we get: