In this post
Area of a triangle As you can see from the table shown previously, the area of any triangle is found by using the perpendicular height multiplied by half of the base. This is shown in visual form below.

The perpendicular height of the triangle must always be at ![]() to the base. Knowing these two values will make it easier to find the area of any triangle.
to the base. Knowing these two values will make it easier to find the area of any triangle.
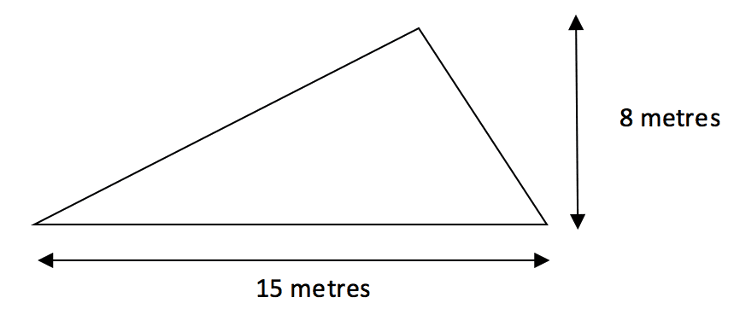
Above we do the calculation ![]() which gives us an answer of 60 metres squared (always remember that the units are now squared units also).
which gives us an answer of 60 metres squared (always remember that the units are now squared units also).
Area of an isosceles triangle
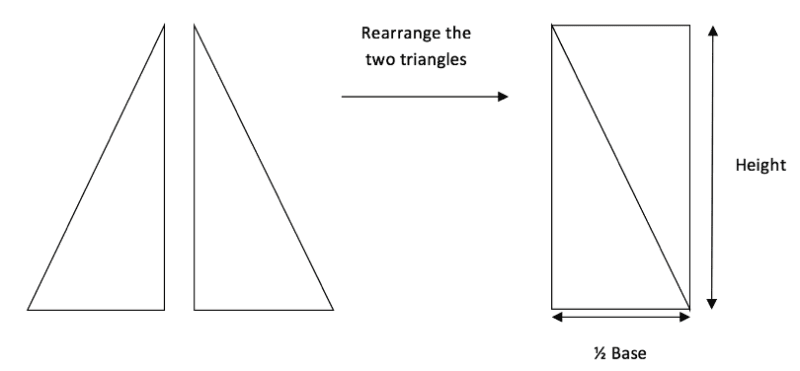
The area of an isosceles triangle is calculated in exactly the same way as we have already discussed, however, we can also see the reasoning behind this method a little clearer with the help of an isosceles triangle.

If we were to split the above isosceles triangle down the middle and then rearrange the two new, right angled, triangles we could create a rectangle as below. It is then easy to see that the area of this rectangle is equal to the original triangle (since we have not added or taken anything away) and has side lengths equal to the height and half of the base of the original triangle. This is where the formula for the area of a triangle comes from.