[vc_row][vc_column][vc_column_text]A composite shape is simply an irregular shape which is made up of several simpler objects. The way to find the areas of these types of shapes is to split them up, work out the individual areas and then add these up to give the total. Previous work on shapes will come in handy when doing this.
Example
Find the area of the shape below if AB=3cm, BC=4cm, AF=6cm and FE=6cm.
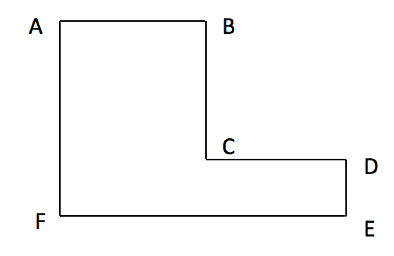
Using the lengths given we can work out all of the sides in this shape as seen below. We can split the shape into two different rectangles, work out each area and add these together to give the total area for the shape above.
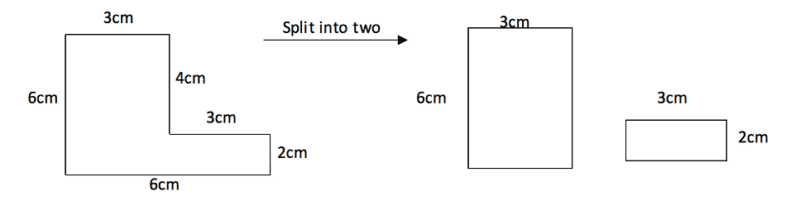
After splitting the shape into two different rectangles, we can find the areas of these and then add them together to give the area of the original.
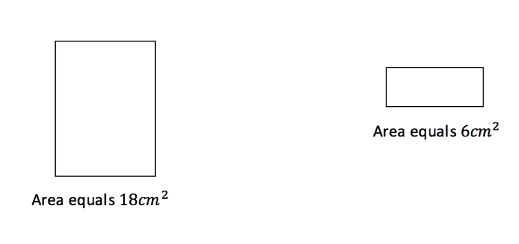
So, the total area of the shape is 
.
Sometimes, instead of adding the areas of shapes, we may need to take parts away.
Example
Find the area of the shaded section in the following diagram of a circle with radius 10cm and square of sides 5cm.
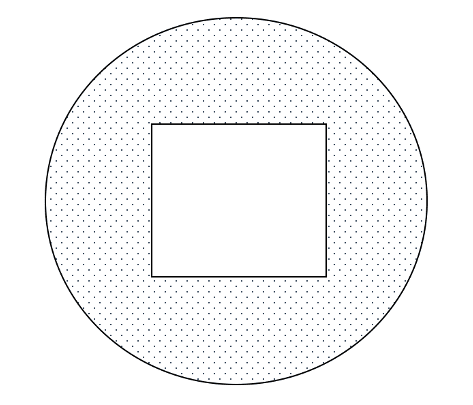
We must find the area of the circle and minus the area of the square. The area of a circle radius 10cm is 
and the area of the square is 
.
So, the shaded part has area 
.
Example
Find the area of the shape below.
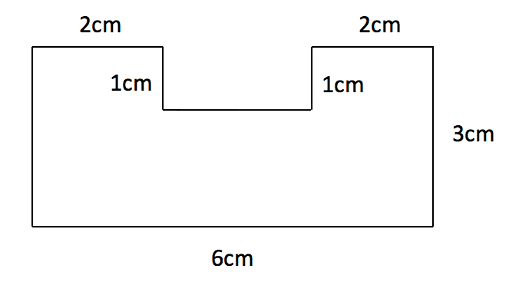
There are several ways of working out this problem: we can either split the shape up into smaller parts and add them together or find the area of the entire rectangle and then minus off the area for the part missing at the top.
By taking the area of the missing part from the whole rectangle we have a shape of area 3cm by 6cm minus a shape of area 1cm by 2cm.
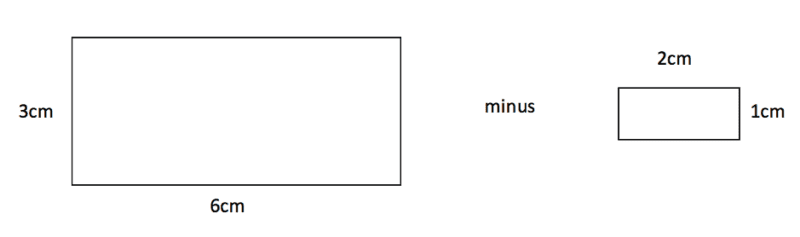
This then gives an answer of 
Another way of finding the area of the original would be to split it into different sections and then add the areas up.
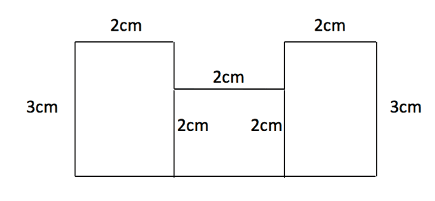
This then gives us three shapes of areas 
, and 
which combine for the entire shape of area 
We have now seen that the way in which a shape may be split up, or if we start with a larger shape and then subtract a certain part, does not matter when working out areas. The most important thing to focus on is splitting the shape up correctly and working out any individual areas in the correct manner.
Perimeters of composite shapes
Finding perimeters of composite shapes can be a surprisingly easy task despite the slightly daunting name! All we need to do is know all of the side lengths and then add these up to give a total perimeter for the shape. It does help to use our knowledge of shapes here so that unknown side lengths can be worked out.
Example
Find the perimeter of the shape shown here.
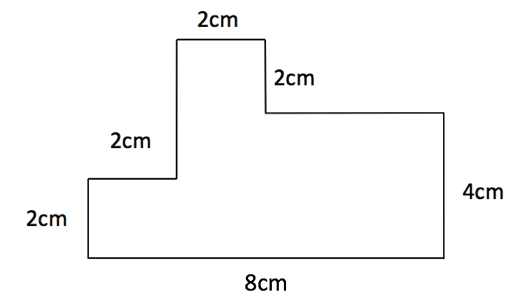
Despite the above example not showing all the individual lengths, we can work these out from knowing the properties of quadrilaterals. So the two missing side lengths are shown below.
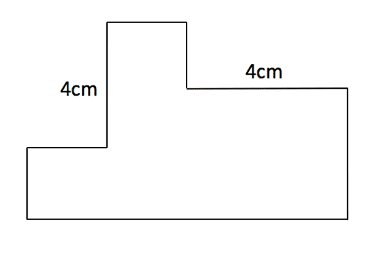
Now we know every side length and can add these up to give the overall perimeter of the composite shape. 
[/vc_column_text][/vc_column][/vc_row][vc_row full_width=”stretch_row_content” css=”.vc_custom_1638196470059{background-color: #113870 !important;}”][vc_column width=”1/6″][/vc_column][vc_column width=”2/3″][vc_row_inner content_placement=”middle” css=”.vc_custom_1638196463239{background-color: #113870 !important;}”][vc_column_inner width=”1/2″][vc_single_image image=”31463″ img_size=”350×350″ alignment=”center” style=”vc_box_border_circle_2″ border_color=”white”][/vc_column_inner][vc_column_inner width=”1/2″][vc_column_text css=”.vc_custom_1649754239493{padding-top: 50px !important;padding-right: 10px !important;padding-bottom: 50px !important;padding-left: 10px !important;background-color: #ffffff !important;}”]
Interested in a Maths GCSE?
We offer the Edexcel IGCSE in Mathematics through our online campus.
Learn more about our maths GCSE courses
[/vc_column_text][/vc_column_inner][/vc_row_inner][/vc_column][vc_column width=”1/6″][/vc_column][/vc_row][vc_section][vc_row][vc_column][vc_column_text][/vc_column_text][/vc_column][/vc_row][/vc_section]
