Dealing with fractions

We have already looked at multiplying and dividing fractions earlier and the exact same methods and principles are used even when we have unknowns in the fraction. We will recap these first.\

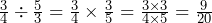
From these easy calculations we can form a rule that is used for all calculations when multiplying or dividing fractions:

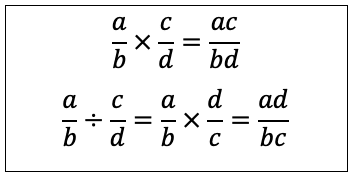
From these formulae we can easily manipulate formulae that involve multiplication and division of unknown values in fractions: we need to just stick to the formulae outlined above.

One thing which we will need to look into, however, is simplifying the fraction once the calculation has been done. Suppose we have the equation  , we can clearly cancel the unknown variable c which appears on the top and bottom of the fraction. This can be done because of the following reasoning:

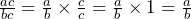
So, for any fraction we must always look for different unknown values that we can cancel from the top and bottom to make sure that the fraction is in its simplest form.

Example

Simplify the following:

First, we must do the multiplications and division shown here then we can think about simplifying the result. Doing the multiplication first we get

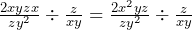
Next, we can swap the end fraction and convert the division into a multiplication which results in:

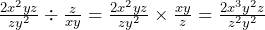
Now all that is left for us to do is simplify the fraction by cancelling any common terms from the top and bottom. The common terms are  and z:

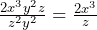
So now the equation that we started with has been calculated and put into its simplest possible form by cancelling any common unknown values.