Decimals

We can use decimals in many ways to do different calculations. The link between fractions and decimals will be explored here and you will become accustomed to recurring numbers and different operations we can carry out using decimals.

Place values

A place value is the relation of where a value is compared to others in that number. For example, 7895 can be broken down into: . So 7 takes the thousands position, 8 takes the hundreds, 9 the tens and 5 the unit value.

This very same method is used when going below 1 and into decimals as outlined here:

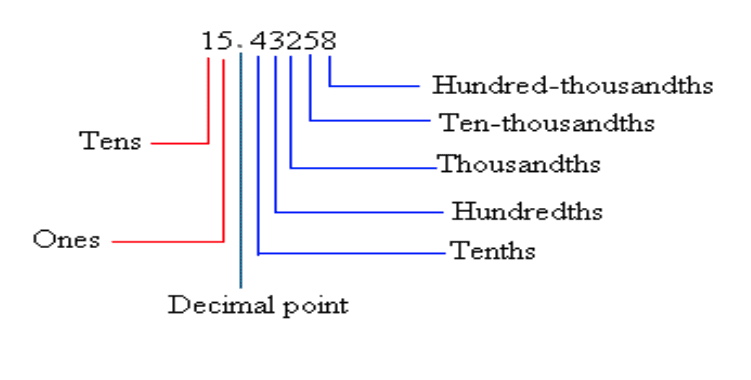
As we go further to the right, the place values decrease, dividing by ten each time. This can also be explained by multiplying by 10 when moving to the left. The decimal 5.97 therefore is the same as  we put each individual number over its corresponding place value.

Zero in a decimal

Whenever we have a zero that is a part of a decimal, we can still use the same approach as above, however, we need to know that zero is called a ‘placeholder’.

This means that it cannot be taken out of the decimal. If we were to do this it would be the same as taking the zero from the number 5709. Clearly 5709 and 579 are very different numbers, as are the decimals 0.5709 and 0.579.

Comparing different decimals

When deciding which of two whole numbers is the biggest it is relatively easy. This is not always the case when we come to look at two different decimals as we need to take into account their place values and if they contain a zero. Even if a decimal has lots of numbers that are individually large, the place value that they hold may be quite small.

For example, 0.1 is larger than 0.0999999. This is because the value of the 1 in 0.1 is higher than the combined values for all the 9’s in 0.0999999.

To find out which of two decimals is the largest we must first look at the tenths place value, then the hundredths and so on.

Example

Is 0.0017 larger than 0.00089?

Since 0.0017 has only two zeros after the decimal point and 0.00089 has three, the 1 in 0.0017 holds a higher value than all of the other numbers combined. Therefore, we know that 0.0017 is larger than 0.00089.

Converting decimals to fractions

When we want to convert a decimal to a fraction we can use the trick of turning each value into a fraction over its place value.

For example, 

By using this trick and what we have already learned on adding fractions with different denominators we can easily convert between decimals and fractions.

Example

a) Write 0.83 as a fraction.

b) Write 1.803 as a mixed number.

Operations with decimals

To add or subtract one decimal from another we need to simply do the same as for any other number, but taking extra care in where the decimal point is. By doing simple addition and subtraction we can use the idea of adding individual digits with the same place values and if this adds up to above 10, then we carry one over.

Examples

Multiplying decimals

To multiply different decimals we can apply a technique where we forget about the decimal point at first and simply multiply two whole numbers. Then we can see how many of the original digits were to the right of the decimal point and adjust our answer accordingly.

For example, if we needed to multiply 7.3 by 0.19, we could work out the answer to 73×1973×19, which is 1387. Now we can see that 7.3 has one value below the decimal and 0.19 has two. So we must divide our answer of 1387 by 10, three times. 1387÷(10×10×10)=1.3871387÷(10×10×10)=1.387.

Really what we have done is recognised that 7.3=73÷107.3=73÷10 and 0.19=19÷10÷100.19=19÷10÷10. Now we can multiply together these two numbers to get the answer:

(73÷10)×(19÷10÷10)=(73×19)÷10÷10÷10=1387÷1000=1.387(73÷10)×(19÷10÷10)=(73×19)÷10÷10÷10=1387÷1000=1.387

So if we were to work out the following:

2.1×0.782.1×0.78     0.21×7.80.21×7.8     0.021×780.021×78

We would find that they all have the same answer of 1.638!

Dividing decimals

When we come to divide two decimals we can convert the equation into a fraction and then multiply both the top and bottom by a number which would make them both whole. We would normally do this by multiplying both the numerator and denominator by a multiple of 10.

Example

a) 0.7÷1.4=0.71.4=0.7×101.4×10=714=120.7÷1.4=0.71.4=0.7×101.4×10=714=12

b) 12.1÷0.11=12.10.11=12.1×1000.11×100=121011=11012.1÷0.11=12.10.11=12.1×1000.11×100=121011=110

Make sure to multiply the top and bottom of a fraction by the same number when using this method.