Factorising equations

How to factorise

In an earlier post we looked at trying to multiply out brackets like . However, we must now try to reverse this in what is called ‘factorisation’. By factorising an equation we put the brackets back in, so we would go from an equation like to  to .

If we have two brackets, as above, and we wish to multiply them out we must add the two numbers in the brackets and make this the coefficient of and then multiply the two numbers to give the number added.

Example

Multiply out the brackets in .

We must find the numbers added together which gives  and the two numbers multiplied which is . Now the sum of the two numbers (the addition) is the coefficient for and the product (the multiplication) is added on to the end. So we are left with .

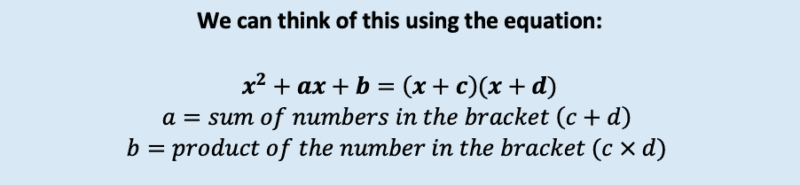
To reverse this process we need to go from know a and b and use them to find out the values of c and d.

This means that we need to find a pair of numbers which will add to make a and multiply to make b  for the following equation:

Example

Factorise the following:

1) 

2) 

3) 

1) Here we need to find a pair of numbers which will add to 6 and multiply to 5. Since 5 is a prime number there are only two numbers that can multiply to make it, 1 and 5. So if we add these two together we will see that they equal 6, which is the value that we need! So the two numbers that we seek must be 5 and 1 to give a factorised answer of 

2) Here we need two numbers that add to 7 and multiply together to give 12. The pairs that will multiply to give 12 are: 1 and 12, 2 and 6 or 3 and 4.  and not 7 so this cannot be the pair,  not 7 so this can’t be the pair either. Finally  which is what we are looking for so the answer is 

3) Here we need two numbers to multiply to 14 and add to 9. The numbers that will multiply to 14 are: 14 and 1 and 2 and 7. Clearly the only one of these pairs that add to 9 is 7 and 2. Therefore the answer must be 

When factorising it does not matter which way around the two brackets appear. So  is exactly the same as .

It is also essential that we check our work and this is easily done. To check for any mistakes we must multiply out the brackets to make sure that this will be equal to the original expression that we were trying to factorise.

Negative and positive numbers when factorising

Factorising expressions becomes harder when we introduce negatives. However, the exact same rules for adding and multiplying with positive and negative numbers are always used in the same way as we learnt in an earlier module. This is recalled here:

positive x positive = positive

positive x negative = negative

negative x positive = negative

negative x negative = positive

The pair of numbers which we use when factorising could both be positive, both be negative or we could have one of each. However, sticking to the above rules we work out the pair in exactly the same way no matter what.

Example

Factorise the following:

1) 

2) 

3) 

1) We need a pair of numbers that adds to give 5 and multiplies to give . To find this we can temporarily forget about the different signs and simply list the numbers that give the product of 6, rather than . These can be 6 and 1 or 2 and 3. Now we can use the fact that the pair must really multiply to , so one of the pair must be negative. Because of one of the numbers being negative we must have a difference between the two numbers (disregarding their signs) of the sum needed, which is 5. Therefore, the answer is clearly 

2) Here we seek two numbers which add  to and multiply to . The pairs to multiply to 8 are 8 and 1 or 4 and 2 and one of the pair must be negative. Again, this tells us that the difference if both numbers were negative must be . Clearly the correct pair is 4 and 2. Now we just need to find which of these is to be negative. The sum of the two numbers is  so we must then set the 4 as negative to get the correct product. So the answer is .

3) Now we seek a pair which multiplies to 7 and adds to . For this to happen we must have two negatives as two positives will multiply to give a positive but add to being positive also. However, a pair of negatives will multiply to a positive and add to a negative which is what we need. The only possible pair to multiply to 7 is 1 and 7. And both of these must be negative! Giving an answer 

When factorising with negatives it is essential that we check the answer again by multiplying out the brackets. When doing this working we will use quite a bit of ‘trial and error’ and it is very easy to make a simple mistake with the working, therefore a quick check can save you from dropping marks.