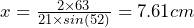Finding the area of a triangle using Trigonometry

April 12, 2022

In a previous post we learnt that the area of a triangle is $\frac{1}{2} \times base \times height$ , and if we draw out a triangle and label the sides and angles we can find a new formula that involves trigonometry.

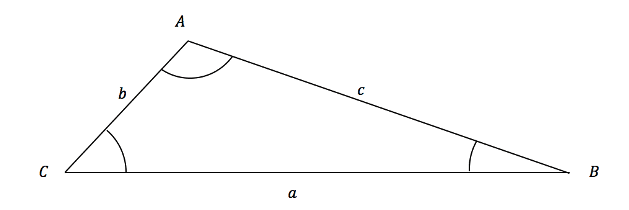
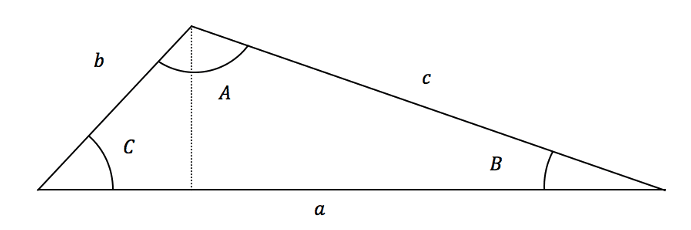
From the above triangle we can draw in the height of the triangle by inserting a line that is at $90^\circ$ to the base and then we see that this triangle is right-angled; this means we can find the height:

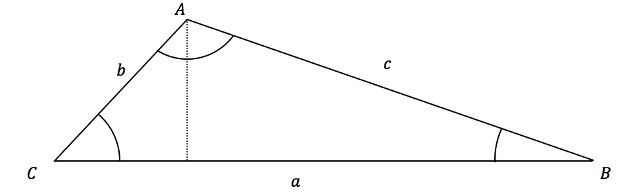
We can now find the length of the dotted line (the height) by trigonometry:

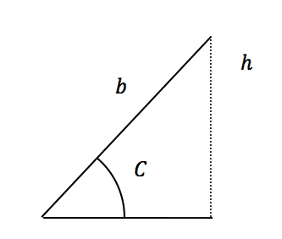
The height h fits into the equation:

sin(C)=\frac{opposite}{adjacent}=\frac{h}{b}

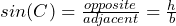
Which makes:

So the height of the triangle below is equal to and the base is clearly the length of a. So we can put these values for the height and base into the equation for the area of $\frac{1}{2} \times base \times height$ which gives us:

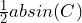
What this formula is telling us is that for any triangle, if we know one angle and two side lengths (that are not opposite the known angle) we can find the area of the triangle by just putting the correct values into the above formula.

Example

Find the area of the triangle shown here:

Here we have the two sides and which we can call a and b as well as the angle $52^\circ=C$ . Putting these into the formula gives:

\frac{1}{2}ab sin(C)=\frac{1}{2} \times 7 \times 17 \times sin(52) =46.89 cm^2

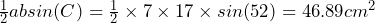
Example

The area of the triangle below is , find the value of x.

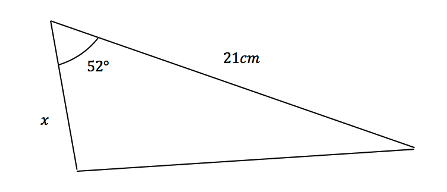
Here we already know the area, the angle C and one of the side lengths. Putting these values into the formula we get:

63cm^2=\frac{1}{2} \times 21 \times x \times sin(52)

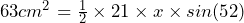
Rearranging and then solving for x gives:

Finding the area of a triangle using Trigonometry

Example

Example

Looking to get a GCSE?

Start your learning journey

Save your cart?