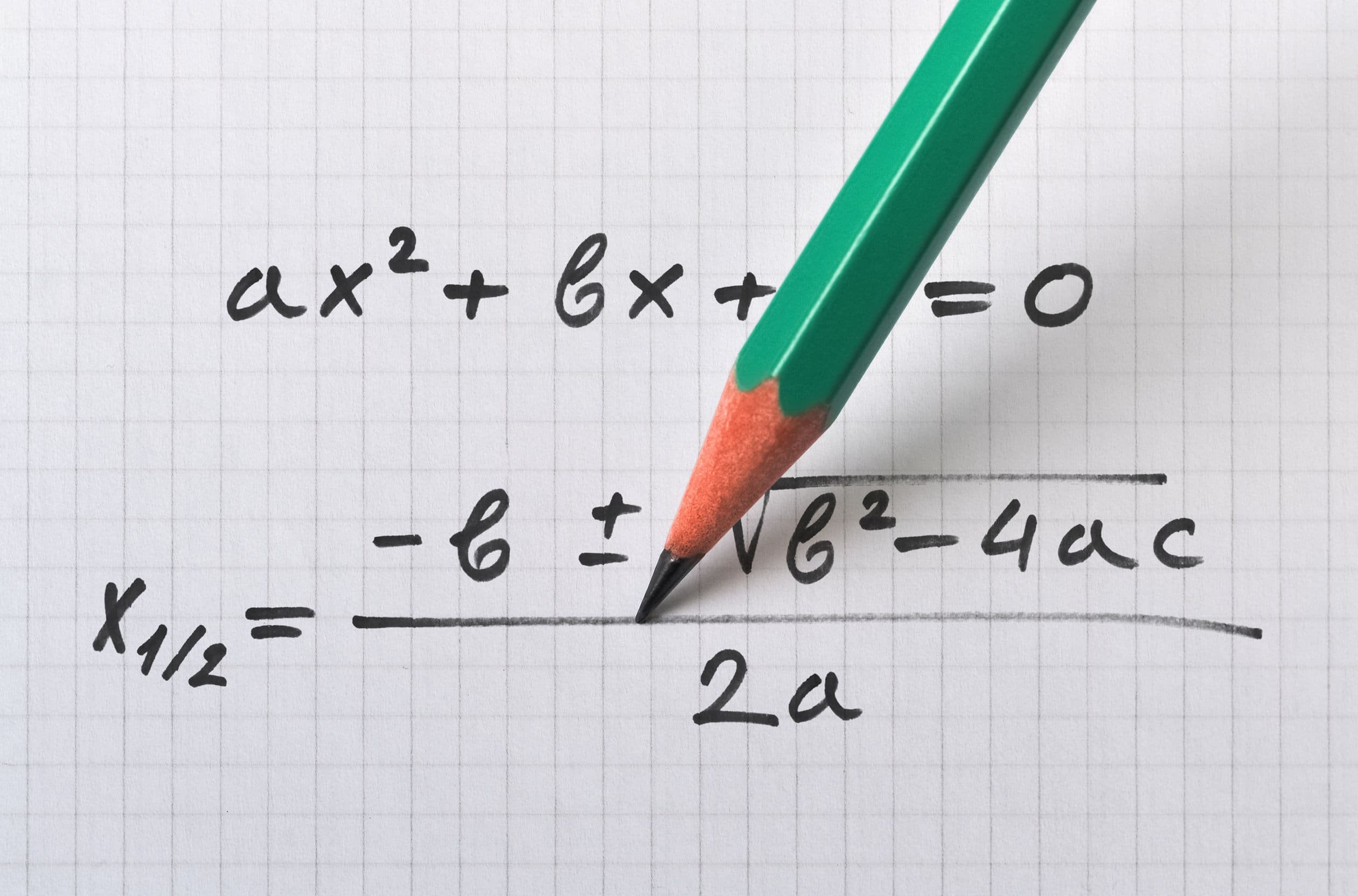Other quadratics
At times we may be faced with a harder type of quadratic which does not have the same layout as we have already seen. So far we have looked at expressions that have just one 
value as opposed to 
or any other coefficient. This poses a much harder problem when trying to factorise the expression into double brackets.
If we have 
 then, when putting in double brackets, we need to have 
 and x like this:
  )(
  )
So now we must find the unknowns to go in these brackets and if they are positive or negative. To do this we must use the same method as earlier and find two numbers which will multiply to 4, however, the sum will be calculated differently since we will have one number multiplied by  and one multiplied by x. To find this there will always be a certain amount of ‘trial and error’ and it helps to draw a table:
| Pair | Product | x term |
|---|---|---|
| 1, 4 | 4 |  |
| 2, 2 | 4 |  |
| -1, -4 | 4 |  |
| -2, -2 | 4 |  |
Clearly the correct pair must be 1 and 4 as these will give the correct term. However, unlike before, the order of these numbers now matters! If we put the two numbers into the brackets we will get:
Which is obviously correct, but if we had the constants (the pair of numbers) the other way around then we would end up with a completely different answer:
Having the pair in the opposite brackets has given us a different coefficient of x! This is because the numbers are multiplied by different values ( or x). So the same pair the other way around will give the same first and last values but the middle value with coefficient x will be different. It goes without saying that extra care should be taken because of this and the result should always be checked. To demonstrate the different values we can get when swapping the constants in the brackets we can extend the table that we had earlier:
| Pair | Product | x term |
|---|---|---|
| 1, 4 | 4 | |
| 2, 2 | 4 | |
| -1, -4 | 4 | |
| -2, -2 | 4 | |
| 4, 1 | 4 | |
| -4, -1 | 4 | |
| -2, -2 | 4 | |
With a little practice you will get used to thinking of the possibilities in your head so that a large table will not have to be made every time.
Interested in a Maths GCSE?
We offer the Edexcel IGCSE in Mathematics through our online campus.
