Hypotheses and Proofs

What is a hypothesis?

A hypothesis is basically a theory that somebody states that needs to be tested in order to see if it is true. Most of the time a hypothesis is a statement which someone claims is true and then a series of tests are made to see if the person is correct.

Key term

Hypothesis – a proposed true statement that acts as a starting point for further investigation.

Devising theories is how all scientists progress, not just mathematicians, and the evidence that is found must be collected and interpreted to see if it gives any light on the truth in the statement. Statistics can either prove or disprove a theory, which is why we need the evidence that we gather to be as close to the truth as possible: so that we can give an answer to the question with a high level of confidence.

Hypotheses are just the plural of a single hypothesis. A hypothesis is the first thing that someone must come up with when doing a test, as we must initially know what it is we wish to find out rather than blindly going into carrying out certain surveys and tests.

Some examples of hypotheses are shown below:

• Britain is colder than Spain
• A dog is faster than a cat
• Blondes have more fun
• The square of the hypotenuse of a triangle is equal to the sum of the squares of the other two sides

Obviously, some of these hypotheses are correct and others are not. Even though some may look wrong or right we still need to test the hypothesis either way to find out if it is true or false.

Some hypotheses may be easier to test than others, for example it is easy to test the last hypothesis above as this is very mathematical. However, when it comes to measuring something like ‘fun’ which is shown in the hypothesis ‘Blondes have more fun’ we will begin to struggle! How do you measure something like fun and in what units? This is why it is much easier to test certain hypotheses when compared with others.

Another way to come up with a hypothesis is by doing some ‘trial and error’ type testing. When finding data you may realise that there is in fact a pattern and then state this as a hypothesis of your findings. This pattern should then be tested using mathematical skills to test its authenticity. There is still a big difference between finding a pattern in something and finding that something will always happen no matter what. The pattern that is found at any point may just be a coincidence as it is much harder to prove something using mathematics rather than simply noticing a pattern. However, once something is proved with mathematics it is a very strong indication that the hypothesis is not only a guess but is scientific fact.

A hypothesis must always:

• Be a statement that needs to be proven or disproven, never a question
• Be applied to a certain population
• Be testable, otherwise the hypothesis is rather pointless as we can never know any information about it!

There are also two different types of hypothesis which are explained here:

An Experimental Hypothesis – This is a statement which should state a difference between two things that should be tested. For example, ‘Cheetahs are faster than lions’.

A Null Hypothesis – This kind of hypothesis does not say something is more than another, instead it states that they are the same. For example, ‘There is no difference between the number of late buses on Tuesday and on Wednesday’.

Subjects and samples

We have already talked in an earlier lesson of different types of samples and how these are formed, so we will not dwell for too long on this. The main thing to make sure of when choosing subjects for a test is to link them to the hypothesis that we are looking into. This will then give a much better data set that will be a lot more relevant to the questions we are asking. There is no point in us gathering data from people that live in Ireland if our original hypothesis states something about Scottish people, so we need to also make sure that the sample taken is as relevant to the hypothesis as possible. As with all samples that are taken, there should never be any bias towards one subject or another (unless we are using something like quota sampling as outlined in an earlier lesson). This will then mean that a random collection of subjects is taken into account and will mean that the information that is acquired will be more useful to the hypothesis that we wish to look at.

The experimental method

By treating the hypothesis and the data collection as an experiment, we should use as many scientific methods as possible to ensure that the data we are collecting is very accurate.

The most important and best way of doing this is the control of variables. A variable is basically anything that can change in a situation, which means there are a lot in the vast majority as lots of different things can be altered. By keeping all variables the same and only changing the ones which we wish to test, we will get data that is as reliable as possible. However, if variables are changed that can affect an outcome we may end up getting false data.

For example, when testing ‘A cheetah is faster than a lion’ we could simply make the two animals run against each other and see which is quickest. However, if we allowed the cheetah to run on flat ground and made the lion run up hill, then the times would not be accurate to the truth as it is much harder to run up a slope than on flat ground. It is for this reason that any variables should be the same for all subjects.

The only variable that is mentioned in the hypothesis ‘A cheetah runs faster than a lion’ is the animal that runs. Therefore, this is called the independent variable and is the only thing that we wish to change between experiments as it is the thing we wish to prove has an effect on other results.

A dependent variable is something that we wish to measure in experiments to see if there is an effect. This is the speed at which something runs in our example, as we are changing the animal and measuring the speed.

Key terms

Independent variable – something that stands alone and is not changed by other variables in the experiment. This variable is changed by the person carrying out the investigation to see if it influences the dependent variables. This can also be seen as an input when an experiment is created.

Dependent variable – this variable is measured in an experiment to see if it changes when the independent variable is changed. These represent an output after the experiment is carried out.

Standardised instructions

Another thing that is essential to carrying out experiments is to give both of the participants the same instructions in what you wish them to do. Although this may seem a little picky, there will be a definite difference in how a subject performs if they are given clear and concise instructions as opposed to given misleading and rushed ones.

Turning data into information

Experiments are carried out to produce a set of data but this is not the end of the problem! We will then need to interpret and change this information into something that will tell us what we need to know. This means we need to turn data in the form of numbers into actual information that can be useful to our investigation. Figures that are found through experiments are first shown as ‘raw data’ before we can use different tables and charts to show the patterns that have been found in the surveys and experiments that have been carried out. Once all the data is collected and in tables we can move on to using these to find patterns.

Proofs

Once a hypothesis has been stated, we can look to prove or disprove it. In mathematics, a proof is a little different to what people usually think. A mathematical proof must show that something is the case without any doubt. We do this by working through step-by-step to build a proof that shows the hypothesis as being either right or wrong. Each small step in the proof must be correct so that the entire thing cannot be argued.

Setting out a proof

Being able to write a proof does not mean that you must work any differently to how you would usually answer a question. It simply means that you must show that something is the case. Questions on proofs may ask you to ‘prove’, ‘verify’ or ‘check’ a statement.

When doing this you will need to first understand the hypothesis that has been stated. Look at the example below to see how we would go about writing a simple proof.

Example

Prove that 81 is not a prime number.

Here we have a hypothesis that 81 is not prime. So, to prove this, we can try to find a factor of 81 that is not 1 as we know the definition of a prime number is that it is only divisible by itself and 1. Therefore, we could simply show that:

The fact that 81 divided by 9 gives us 9 proves the hypothesis that 81 is not prime.

A proof for a hypothesis does not have to be very complex – it simply has to show that a statement is either true or false. Doing this will use your problem-solving skills though, as you may need to think outside the box and ensure that all of the information that you have is fully understood.

Harder examples

Being able to prove something can be very challenging. It is true that some mathematical equations are still yet to be proved and many mathematicians work on solving extremely complex proofs every day.

When looking at harder examples of proofs you will need to find like terms in equations and then think about how you can work through the proof to get the desired result.

Example

Prove that 

Here we need to use the left-hand side to get to the right-hand side in order to prove that they are equal. We can do this by expanding the brackets on the left and collecting the like terms:

We have now expanded the brackets and collected the like terms. It is now that we will need to look at our hypothesis again and try to make the above equation into the right-hand side by moving terms around. We can see from the right-hand side of our hypothesis that we have a double bracket and then 2 added to this so we can begin by bringing 2 out of the above:

Now we simply need to check that  which is easily done using our knowledge of expanding brackets.

So we have now worked through an entire proof from start to finish. Here it is again using only mathematics and no writing:

Prove that 

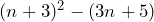
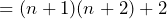
In the above we have shown that the hypothesis is true by working through step-by-step and rearranging the equation on the left to get the one on the right.

Example

Prove that 

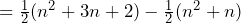
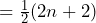
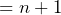
Above we have worked through the problem step-by-step through our knowledge of collecting like terms and multiplying out brackets. Then we have used the hypothesis that we are trying to prove in order to cancel out certain terms and get to our answer of .

The step-by-step approach to proofs

To prove something is correct we have used a step-by-step approach so far. This method is a very good way to get from the left-hand side of an equation to the right-hand side through different steps. To do this we can use specific rules:

1) Try to multiply out brackets early on where possible. This will help you to cancel out certain terms in order to simplify the equation.

2) Use the hypothesis to direct your work. Once you have multiplied out the equation you can look at your destination in the hypothesis in order to understand what you are trying to achieve. It may be that your destination has a specific term such as  that you will need to bring out of the equation. It is much easier to prove a hypothesis when you keep your final result in mind at all times to understand where you should be heading.

3) Take small steps each time. A proof is about working through a problem slowly so that it is easy to spot what has been done in each step. Do not take big leaps in your work such as multiplying out brackets and collecting like terms all at once. Remember that the person marking your paper needs to see your working, so it is good to work in small stages.

4) Go back and check your work. Once you have finished your proof you can go back and check each individual stage. One of the good things about carrying out a proof is that you will know if a mistake has been made in your arithmetic because you will not be able to get to the final solution. If this happens, go back and check your working throughout.

Harder proofs

When working through a proof that is more difficult it can be quite tricky. Sometimes we may have to carry out a lot of different steps or even prove something using another piece of knowledge. For example, it might be that we are asked to prove that an expression will always be even or that it will always be positive.

Example

Prove that  is an even number.

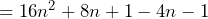
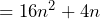
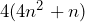
In the above equation we have worked through to get an answer that is completely multiplied by 4. This must therefore be even as any number (whether even or odd) will be even when multiplied by 4.

In this example we have had to use our knowledge that anything multiplied by 4 must be even. This information was not included in the question but is something that we know from previous lessons. Some examples of information that you may need to know in order to solve more difficult proofs are:

Any number that is multiplied by an even number must be even

A number multiplied by an even number and then added to an odd number will be odd

Any number multiplied by a number will give an answer that is divisible by the same number (e.g. 3n must be divisible by 3)

Any number that is squared must be positive

Example

Prove that, when is any natural number, must be positive.

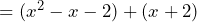
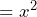
Working through this problem has given us an answer of  which we know is positive because any natural number squared must always be positive in value.

Example

Prove that  is divisible by 3.

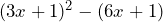
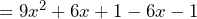
Above we have come to an answer that is multiplied by 3. This means that the answer has to be divisible by 3 also.