Indices

In this post

A number, when multiplied by itself, can be written as a square. This works for all numbers and is shown as: (using 10 as an example) $10 \times10=10^2$ . This in fact can work with any different ‘index’ so we can write $10 \times10 \times10$ as $10^3$ and in the same way for any amount of the same number being multiplied by itself. An index (indices is the plural) shows us the number of times that a number is multiplied by itself.

As we have already said, any number can also be written with an indices of 1. So the number 7 can actually be thought of as $7^1$ and the same applies for any other number.

But what if we were to have a number with the indices being -1?

When we have an indices that is a minus number, this can be written as a fraction!

So $6^{ - 1}$ is the same as $\frac{1}{{6 }}$

And $6^{ - 2}$ equals $\frac{1}{{6 \times6 }}=\frac{1}{36}$

Rules for indices:

The number that is the indices tells you the amount of multiplications that we must do:

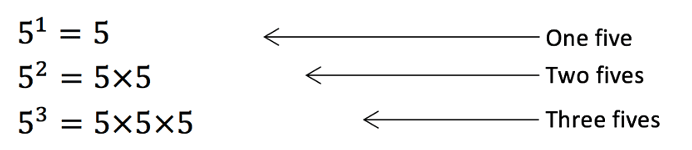
If the indices is negative, then we take the reciprocal (which was learnt in the last lesson) of the number:

$5^{-2}=\frac{1}{5^2}=\frac{1}{5 \times5}=\frac{1}{25}$

This works for any value of the reciprocal and is summarised as the rule:

$Rule for indices in a fraction$

Where a and b can be any number.

(do not worry too much if you do not understand this notation yet)

Multiplying and dividing indices

To allow us to multiply or divide two numbers that are in index form, first they must have the same base. The base of an indices is the number which is being multiplied, so the base of $4^3$ is 4. If the two indices do not have the same base then we cannot use the rules which will be outlined here. For example, $4^3 \times5^6$ cannot be found using these rules of indices.

Multiplying

When multiplying indices with the same base we simply add the powers together. So if we were to multiply $3^4$ by $3^5$ :

$3^4= 3 \times3 \times3 \times3$

$3^5= 3 \times3 \times3 \times3 \times3$

$3^4 \times3^5 = (3 \times3 \times3 \times3) \times(3 \times3 \times3 \times3 \times3)$

$3^4 \times3^5=3^9$

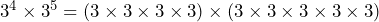
So we have shown that $3^4 \times3^5=3^{4+5}=3^9$

Dividing

To divide two indices we must take the indices away. So if we were to divide $4^6$ by $4^2$ :

$4^6=4 \times4 \times4 \times4 \times4 \times4$

$4^2=4 \times4$

$4^6 \div4^2=\frac{4\times4 \times4 \times4 \times4 \times4}{4 \times4 }$

$=4 \times4 \times4 \times4=4^4$

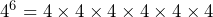
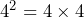
This has been done by cancelling the fraction as seen above.

So we have shown that $4^6 \div4^2=4^{6-2}=4^4$

One more trick for working out an answer when two indices are operated, is for when we wish to calculate something like $(2^2)^4$

This is where we have an index within another index. If we think about it logically, what we are searching for is $(2^2) \times (2^2) \times (2^2) \times (2^2)$ where $(2^2)=2 \times2$

If we worked through this, we would find that the answer is $2^8$

This is because when we have two indices like this, we multiply them together. So $(2^2)^4=2^{2 \times4}=2^8$

Rules for indices


Operation	Rule	Example
Multiplying	Add the powers	$3^3 \times3^4=3^{3+4}=3^7$
Dividing	Minus the powers	$4^8 \times4^5=4^{8-5}=4^3$
Two indices	Multiply the powers	$(5^3)^5=5^{3 \times5}=5^{15}$

Indices on a calculator

Most modern scientific calculators will have a ‘squared’ button, so to do the calculation $5^2$ you simply type a 5, followed by the squared button and then equals.

However, when calculating indices that are not simple squares we must use a different button, which is usually shown as $x^y$ on a calculator. To use this we type the ‘base’ number of our problem, then the $x^y$ button, then the power and finally equals.

So to find $6^4$ we type: $6x^y4=$

All calculators vary and you should read the instructions with yours to make sure that you know where this button is located. Practise using it to become accustomed to doing these types of calculations.

Zero as an indices

Whenever we have 0 as an indices, this automatically means that the answer is 1. Therefore $7^0$ is the same as $3^0$ or any other number with a different base but index of 0. Since they all have just 0 as an indices, they are equal to 1.

This means that when multiplying by a power of zero, we can convert to a 1 and the operation does nothing to other values.

Example

$5^4 \times5^0=5^4 \times1=5^4$

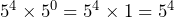
Standard form

Standard form is a technique that involves indices and helps to write very large or very small numbers in a simple way. In this method we use a number between 1 and 10 that is multiplied by 10 to the power of another number. Essentially what we are doing here is taking a very simple number and then moving the decimal point by multiplying this by 10 as many times as needed.

A $\times10^n$

Using the equation shown above we can see that A will be a number between 1 and 10 and the indices n will tell us the number of places the decimal point must be moved.

Example

Write 18,000,000 in standard form.

Here we have the number 18 million which we must write in standard form. To do this we need to find a number between 1 and 10 that can be multiplied by 10 a certain number of times to give 18,000,000.

This can be written as $1.8 \times10000000=1.8 \times10 \times10 \times10 \times10 \times10 \times10 \times10 =1.8 \times10^7$ .

We can also use this same method for numbers that are very small. When doing this we use the same idea but have a negative indices instead of a positive since this is a way to decrease the number. As we know, multiplying by $10^{-1}$ has the same impact as moving a decimal place to the left.

Example

Put the number 0.0000782 into standard form.

Here we need to make the number bigger in order to get our value between 1 and 10. However, we can see from the number that this should be 7.82 once the decimal place has been moved enough.

$0.0000782=7.82 \div10 \div10 \div10 \div10 \div10 =7.82 \times10^{-5}$

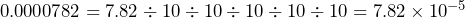
So we can see that we get the answer of $7.82 \times10^{-5}$ .

Tricks with standard form

It is often the case that standard form is used when working with microscopic measurements as it is easier to write the standard form rather than a very long number. In physics you will see standard form being used for distances between planets or even things like the speed of light which is approximately 300000000 metres per second. Rather than writing this number, physicists simply use the standard form of $3 \times10^8$ .

Not only can standard form make it easier for us to display very large or small numbers, it can also come in useful when we are manipulating these numbers. If we were to add or subtract numbers in standard form there is no trick that we can use – we have to change the values back into numbers and then do the calculations. However, when multiplying or dividing we can save time by using a couple of tricks that we know from earlier in this lesson:

To multiply powers you add (for example $10^3 \times10^6=10^9$ )

To divide powers you subtract (for example $10^7 \div10^2=10^5$ )

These two rules work very well when we are working with standard form as we can multiply or divide the base number and then either add or subtract the powers.

Example

Multiply $2.3 \times10^4$ by $7.7 \times10^3$

Here we have a multiplication so the indices can be added while the bases of 2.3 and 7.7 are multiplied as normal. This gives us $17.71 \times10^7$ . Obviously, our base is now no longer between 1 and 10 which we must address by moving the decimal place to the left – which is the same as increasing the power by 1.

So we have a final answer of $1.771 \times10^8$ .

Example

Divide $6.2 \times10^7$ by $2 \times10^2$

On this question we need to take 2 from 7 to give us the indices and divide 6.2 by 2 for the base. This gives us a value of $(6.2 \div2) \times10^{7-2}=3.1 \times10^5$

On this occasion we do not need to adjust the answer as the base is between 1 and 10, so our final answer is $3.1 \times10^5$ .

Interested in a Maths GCSE?

We offer the Edexcel IGCSE in Mathematics through our online campus.

Learn more about our maths GCSE courses