Interest

Interest is given on investments that you make and is calculated as a percentage of the initial investment. For example, an investment of £1000 may receive interest at 5% for 6 years in a certain case.

There are two types of interest which we will be looking at on this course: simple interest and compound interest. These two are outlined below.

Simple interest

Simple interest is calculated on an initial investment and paid back to the investor yearly. This means that for any investment, a certain amount will be paid every year and the amount will always be the same.

Example

A simple interest rate pays 5% per annum. Calculate the amount of money made with the following investments:

a) £350 for 2 years

b) £700 for 5 years

c) £500 for 3 years

a) To calculate this we must find 5% of £350, which is done using methods explored earlier to get £17.50. This amount is then paid out every year for 2 years and so the investor receives a total of £35.

b) Here we again need to find 5% but this time of £700 and for 5 years. 5% of £700 is £35, which is paid 5 times so the total amount received is £175.

c) 5% of £500 is £25, and this is received for 3 years in total so the investor gets £75.

So to work out the total money that will be received for a simple investment we just have to find the correct percentage of the investment and multiply by the number of years the investment is for.

Compound interest

A different way of calculating interest is if we use the method of compounding the interest so that instead of receiving the money on an investment, it is put back into the account and generates interest itself.

This is much harder to work with than simple interest as the interest amount will be different every year when the money in the investment increases. To calculate the total when interest is compounded we must work out the investment and total money in the account for each individual year. This is shown in the example below.

Example

An investment of £2000 is made for 4 years with interest at 5% compounded annually. How much money is made?

Year	Total at start of year	Interest for year	Total at end of year
1	£2000	5% of £2000 = £100	£2100
2	£2100	5% of £2100 = £105	£2205
3	£2205	5% of £2205 = £110.25	£2315.25
4	£2315.25	5% of £2315.25 = £115.76	£2431.01

So the total amount of money after the 4 years is £2431.01.

Clearly, to work out the return on an investment that is compounded is much harder than for a simple interest rate. This is because the interest previously earned also earns interest the next year. So, generally, an investment with compounded interest gives more money to the investor in the same time period. Of course, the drawback of this is that you will not receive payments every year, you will have to wait until the very end of the investment to get the interest back.

Quicker methods for calculating interest

A slightly quicker way to calculate the interest on a sum of money is to convert the percentage given into a decimal. However, when doing this you must make sure to take note that the original value is included, so the decimal will be above 1 for a positive interest account.

With the use of a decimal rather than a percentage for interest we can use a formula that helps us to save time when calculating compounded interest. This is shown below:

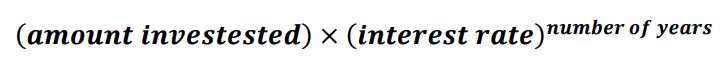
Using this formula we can work out the amount received with a compound interest investment for any number of years. Clearly this is a much easier sum than writing out a table and working out the value of each year separately, however, you should know how to do both before your exam. To use the power button on a calculator refer to the instructions as each model may be different.

Example

Calculate the total return on an investment of £4000 at 6% interest per annum for 4 years.

Using the formula from above we can easily work out the answer:

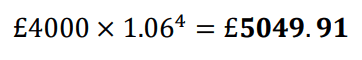
To get the correct answer we must remember that the ‘interest rate’ in the formula is not simply 6%, but the original included, so the rate is 106% or 1.06.

Depreciation

This is the same as having negative interest and will usually apply to things like cars and other goods that are purchased. Over time items become older and their value decreases; this amount can be calculated with the use of depreciation. You must always remember that an amount must decrease with depreciation and so an amount needs to be multiplied by a value less than 100%.

Example

Omar buys a new car for £6000. If the car’s value depreciates by 10% per year, how much would he expect to sell it for after 4 years?

This problem can be solved using the table as before or by using the formula outlined. Since using the formula is much quicker we will do this: .

The depreciation is 10% therefore we have used 90% or 0.9 as the interest rate.

Reverse calculations

Sometimes we will be required to ‘work backwards’ to get an original price/value after an increase or decrease of the original value.

Final value = Original Value × Multiplier

The above is the equation that is used for finding a value when an original is altered in some way to a new value. To reverse this and get the original from the new value we must use our knowledge that a multiplication is the opposite of a division. Then we can rearrange this equation to make the original value the subject:

Original value = Final Value ÷ Multiplier

Original Amount	% change	Increase or Decrease	Multiplier	Final Value
1000	5	Increase	1.05	1050
368	6.5	Decrease	0.935	344.08
821.5	3.1	Increase	1.031	846.97

The above table shows a few examples of percentage increases and decreases and how the multiplier used is formed. If we are increasing by a percentage then the equivalent decimal is added to 1 and this is the multiplier that is used. However, if we are decreasing by a percentage the equivalent decimal is taken away from one to give the multiplier. This is because the full 100% of the amount is equal to a multiplier of 1 and will have no impact on the amount.

If we were to get back to the original amount from this final value (and we know the multiplier) we can easily use the inverse and divide the final amount by the multiplier used. This is shown in the table below for the same amount as above.

Final Amount	% change	Increase or Decrease	Multiplier	Final Value
1050	5	Increase	1.05
344.08	6.5	Decrease	0.935
846.97	3.1	Increase	1.031

Combinations of increasing and decreasing

If we were told that there was to be a combination of increases and decreases then we may be tempted to work out the values after each step and use the new value to compute the next. However, instead of doing this we could work out each individual multiplier and then simply multiply them all together. This will save us a lot of time and effort and mean that we can just multiply the original value by the different multipliers to get the entire final value.

Example

A stock that is worth £85 increases by 4%, then decreases by 11% and then increases again by 6%. What is its final value after all of the changes?

To do this we could work out what a 4% increase of £85 is. This is £88.40 which is then the new value and needs to be decreased by 11%. Solving the problem this way is completely valid but a faster way is to find all of the individual multipliers and then times all of these together and then by the original value of £85. An increase of 4% has a multiplier of 1.04, decreasing by 11% is the same as multiplying by 0.89 and increasing by 6% is the same as 1.06. So all that we need to do is multiply each of these by the original amount.

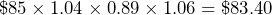
This method has clearly saved us a lot of time in our calculations and still gives the correct answer.

Example

An investment increases at a rate of 5% for 4 years before decreasing by 3% for 2 years. If I invest £100, how much do I have after the full 6-year investment?

Here we will still use the method of multiplying together the multipliers as in the previous example but we can also make use of indices to show the number of years at a certain rate. So we can make a sum where we multiply the original amount by each of the multipliers to the correct power.

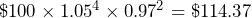
The multiplier for an increase of 5% is obviously 1.05 and this is to the power of 4 as the increase lasts for 4 years. Then the multiplier for a decrease of 3% is 0.97 and this lasts for 2 years and so has an indices of 2.

Growth and decay

Something that is related to interest and depreciation are growth and decay rates. These are worked out in the same way as interest and depreciation, so we need a starting amount and then a multiplier which is often a percentage. We then also need a length of time that we are measuring the growth or decay over.

Example

The numbers of deer in a forest is decreasing by 8% each year due to trees being chopped down and hunting. If there are 3500 deer in 2010, work out how many there are in 2015.

In this question we know that the population of deer is decreasing by 8% each year – this means that we can use 0.92 as our multiplier as this is 8% less than 1. We also know that we are working out the population over 5 years from 2010 to 2015 so this is our length of time. We also know that in 2010 there are 3500 deer. Using this information we can use the same formula as previously to find out how many there are in 2015:

When using this formula we must be careful to multiply the indices by the decay or growth rate first. By using our rules of BODMAS we will be able to work out the correct answer and complete calculations in the right sequence.

Example

The numbers of fungus that are found in a forest are increasing. Currently the fungus occupies 20 square km of the forest which is 100 square km in total. The rate at which the fungus grows is 12% per year. Find out how much of the forest is covered in the fungus after 4 years as a percentage.

In this question we can use the same formula to calculate the amount of the forest that is covered after 4 years:

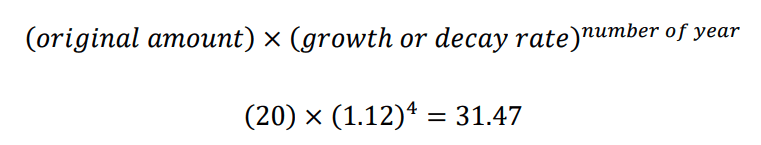
By using the 12% increase for the fungus and converting this to 1.12, we can calculate the coverage of the forest after 4 years to be 31.47 square km. Since the forest is 100 square km we can then convert this amount into a fraction of the total area which means that, after 4 years, the fungus has grown to cover 31.47% of the forest.