A locus (loci is the plural of this word) is simply a path. The path that something takes will be dictated by rules that are set out in a situation. For example, we may say that a locus shows where a person walks through a park and states the distance they are from certain objects.
Often when drawing loci we are told to ensure the path is a fixed distance from something else. For example, we may be told to draw the locus that is a fixed distance of 5cm from a point. This would result in a circle being drawn with a radius of 5cm which is shown below:
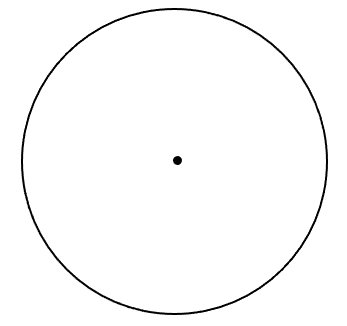
Since a locus can be a line, circle, square or any other shape, we can draw out a wide variety of situations. Another common locus that you may be asked to draw is a path that something takes which is an equal distance from two points. To do this we simply draw a line that bisects the line created by the two points we are working with. This is shown below:
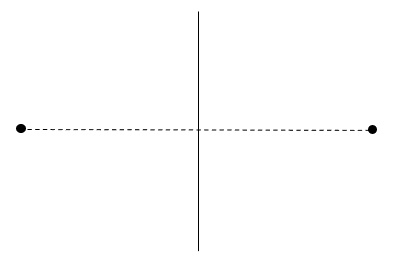
In order to draw a locus that remains a constant distance between two points we can link the points (this is shown with the dotted line in our diagram). Next, we need to find a line that is a perpendicular bisector of this dotted line. To do this we can easily use the techniques that we have learnt a little earlier in this part of the course. This will leave us with a line that cuts right down the middle of the two points and, no matter what point is selected on this line, it will always be an equal distance from one point to another.
Example
A dog is tied to a 4-metre-long metal bar by a 2-metre-long lead while his owner goes into a shop. Draw the locus of where the dog can walk to.
Here we need to draw a locus that is constantly 2 metres from a line that is 4 metres in length. To start with, we can begin by drawing the metal bar which is 4 metres:
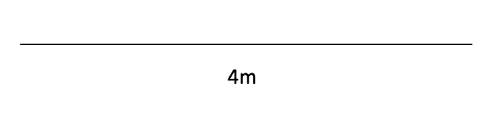
Using this diagram we can move on to draw the locus that is constantly 2 metres from the bar. This is shown in the diagram below:

From the above we can see that the blue line is the locus that is 2 metres (not to scale) from the metal bar. This means that it constantly remains the same distance from the line, even at the ends where the locus is found in the same way as for a point. This results in straight sides and rounded edges.



