In this post
Measurements of flat objects are separated into two different types: perimeters and areas. These two are closely related and we can work out one if we already know the other. Both will be used to further our knowledge when we come to study volumes in a later section.
Perimeter
A perimeter of a shape is simply the length of all the sides added together. Therefore, we can think of this as the distance that we would have to travel around an object, sticking to the edges, until we would return to the original place from which we started.
The perimeters of shapes such as a square or rectangle can easily be found using the properties of these shapes, which we already know.
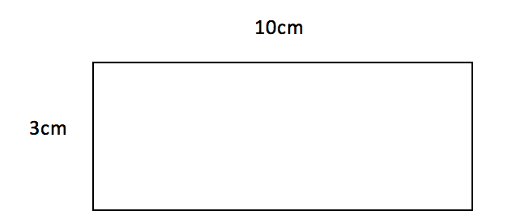
For the rectangle above we can use the fact that opposite sides are equal, so we will have two sides of length 3cm and two sides of length 10cm. Then when we add up all of the side lengths we will get the answer for the perimeter as ![]() .
.
This same technique can be used for a square or any other regular polygon which we have already studied, as long as the side that is given can be used to work out all of the sides of the shape. The perimeters of triangles can also be found using the properties of these three-sided shapes that we have already looked at to find all sides and then add these together for the perimeter.
Finding the perimeter for a circle is a little more complicated. Any circle’s perimeter has a different name: it is called the circumference of the circle. To work out this circumference we need to know the diameter, which is then multiplied by ![]() (approximately 3.14).
(approximately 3.14).
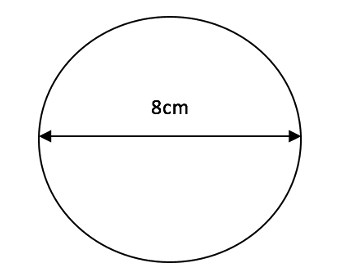
To find the perimeter of the circle above, which has a diameter of 8cm, we need to multiply this by the value of pi (![]() ).
).
This gives us: ![]() to two decimal places.
to two decimal places.
Area
The area of a shape is the amount of room that it takes up. For example, a football pitch or a table top may be measured as an area to see how much space there is on it.
To find an area we must calculate how many equal sections can fit onto it but the units which we use must be squared also. Taking the same example of a rectangle on the previous page we can find the area.
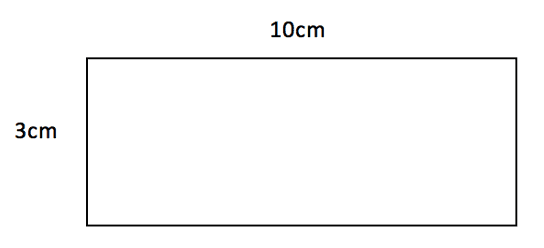
Here we have 3cm by 10cm so the area must be equal to ![]() . As you can see, the two side lengths are multiplied and the units (cm) are squared. This tells us that the area is the same as having 30 different squares each of size 1cm by 1cm.
. As you can see, the two side lengths are multiplied and the units (cm) are squared. This tells us that the area is the same as having 30 different squares each of size 1cm by 1cm.
There are certain techniques that are used to find areas of shapes, as not every area is as simple as that of a rectangle. The most important of these are listed below.
| Shape | Area |
|---|---|
| Rectangle or square | length |
| Triangle | |
| Circle |



