Probability

Total probability

Suppose that instead of having just one outcome, we wanted to find the value for getting one of two possible outcomes. This could be if we wanted to know the possibility of getting a 1 or 2 when rolling a six-sided dice. To do this we must simply add the two separate probabilities, for 1 and 2, to give us the probability of . The same method is used for adding any more possible outcomes, so for 1, 2 or 3 to be found we have a probability of .

This can then be used to show that the total probability of all outcomes must be equal to 1. Since, with the example of a dice, we would have six different sides each of probability  meaning that the probability of getting any side is . This makes sense as we have to get one of the numbers when rolling a dice! This then can go on to tell us that, if we have all possible outcomes that are of equal probability, then each possibility must be  where n is the number of different possibilities.

Dice number	1	2	3	4	5	6
Probability

The probability of an event not happening

Since we know that the total probability of every event must add up to 1, we can quite easily look for a probability of something not happening. To do this we must simply minus the appropriate probability from the grand total of 1. For example, say we wanted the probability of rolling a dice and not getting a 5, we would work out  . The same can be done if we want to find the probability of not getting 2 or more different outcomes, we would simply minus off both of these probabilities.

Example

A bag contains ten counters, three of which are brown, six are pink and one that is blue. If I pick one at random, find the probability of: a) NOT getting a pink and b) NOT getting a blue or brown.

a) Here we need the probability of not getting a pink, which make up 6 out of the 10 counters. Therefore, the probability of picking a pink counter must be . If we take this value from 1 we are left with the probability of not getting a pink which is or  or .

b) Here we need to begin by finding the probability of getting a blue or brown, which have respective probabilities of  and so combine to give , taking this away from the total of 1 gives or  or 

Different ways of expressing probabilities

Clearly, we can express probabilities as fractions as we have already seen. Therefore, a probability can be changed into a decimal or fraction also using techniques we have already learned on this course.

Probabilities can also be shown as being the amount of times we would expect to get a certain result out of a number of tries. So we could say that when flipping a coin, we expect to get heads every ‘1 in 2’. The trick to finding the possibilities from this is to simply convert to a fraction, so ‘1 in 2’ becomes .

The most important thing to remember when working with probabilities is that we are looking for a relation between the total number of outcomes and the outcome that we are looking at. From this we can then form numerical representation that can be used in our working.

Experimentation

When carrying out an experiment that we know, probabilities for the result may sometimes surprise us! Just because we have a chance of getting a head 50% of the time when flipping a coin does not mean that after 10 tries we will get 5 that are heads. We may get 6, or 4, or even no heads at all when we do the experiment. However, when doing an experiment a large number of times, we would expect that the number of an outcome would be related quite closely to the probability that we had to start with.

Mutually exclusive events

If two possibilities are ‘mutually exclusive’ it means that they cannot both happen together. For example, if I were to flip a coin, the outcomes of heads and tails are mutually exclusive as there is no way that I could get both a head and a tail as the result of the same flip.

The OR rule

When we are asked of the probability of one event OR another, we can simply add the two together. However, the two events MUST be mutually exclusive for this method to work.

We can show this by saying that:

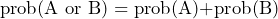
We can use this rule throughout our work on probability and can save quite a lot of time by doing so. The above equation is not only true for two events – it is true for any number of situations as long as these are all mutually exclusive. So, we can use the equation:

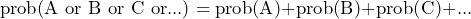
By using this knowledge we can work out the probability of any one of a number of events occurring if we only know their individual probabilities. Not only can we calculate the probabilities of events in this way but we can also find the probability of things not happening. This is done using the rule that, for two mutually exclusive events A and ‘not A’ we can use the formula:

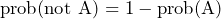
From this formula we can easily work out the probability of not being able to achieve an outcome. For example, if we know that there is a 0.2 chance of rain tomorrow, we can easily work out the chance of it not raining to be:

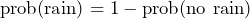
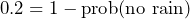
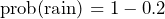
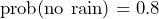
Exhaustive sets

An exhaustive set is where we have a list of possible events where one or more must occur. An example of this is when a dice is rolled. In this situation we have an exhaustive list of outcomes as we can get a 1, 2, 3, 4, 5 or 6 but nothing else. Because no other possible outcome can occur, the possibilities in an exhaustive set must add to 1 if all of the possibilities are mutually exclusive. Using our example of rolling a dice we can show this as:

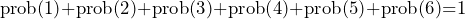
Expected frequency

The expected frequency of an event is related to its probability and the amount of trials that we run. The trials are simply the amount of times we do something for which the probability is always the same, from the first time to the last. An expected frequency will give us the amount of times we could expect something to happen for the amount of attempts that we make. As said earlier, this does not guarantee that we will get exactly this amount, as probabilities do not always go to plan!

The expected frequency can be calculated by:

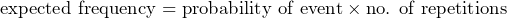
Using the same example as before, if we were to flip a coin 20 times, the expected probability of getting heads would be:

 repetitions 

So we would expect to get a result of heads 10 times out of the possible 20. The expected frequency is relatively easy to calculate but, as we have already said, this is not a definite number and is only the most probable outcomes. This does not mean that we will get exactly this amount of results from the experiment!

Independent events

Another thing that we can find when working with probabilities is an event that is independent of another. This means that an outcome will not be affected at all by something else that is going on. For example, if we roll a six-sided dice and flip a coin, the two events will not have any effect on the outcome of the other. The number that is found on the dice will have no impact on the way the coin lands, so the two events are said to be independent. This is different to a dependent event such as picking two cards from a deck and not replacing them. The second pick in this case is affected by the first as this first card has already been removed so there are now only 51 cards to choose from.

The AND rule

Another rule which is similar to the OR rule is the AND rule. The AND rule instead is used when looking at two ‘compound events’; this means two events that must both happen. The two events have a chance of both happening and this is the probability that we look to find.

An example of this would be to flip a coin and try to get heads twice in a row. We will be looking at the probability of the first head and the second which is harder to do than to get just one head when flipping the coin. The two events that are working together in the AND rule must be independent (so one must not affect the possibility of the other). This is the only way that the AND rule will work.

For example, if we flip a coin twice, the result of the first flip has no impact on the result of the second, therefore they must be independent and the AND rule can be used.

The AND Rule:

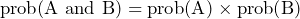
As you can see from the formula above, when using the AND rule we must multiply the two probabilities of separate events to get the probability of both happening. This should not be confused with the OR rule which adds the two probabilities together.

Example

I flip a coin twice. What is the probability of getting two tails?

The probability of getting a tail on the first flip is 0.5 as we already know since there are two possibilities that are equally as likely. So we need to find the probability of two tails which each separately have a probability of 0.5. From the equation above we see that we must multiply the two probabilities to get the value for flipping the coin twice and getting two tails. So .

Example

Again, I flip a coin twice. What is the probability of getting a head and a tail in any order?

The probability of a head is 0.5 and the probability of a tail is 0.5, so the probability of getting both uses the AND rule and must be . However, for this question we must be more careful as we can have these two outcomes in any order. This tells us that we can have either heads then tails or tails then heads. The order of the outcomes does not matter! So we must also use the OR rule to get the probability of getting heads then tails OR tails then heads. Both of these have a probability of 0.25 and using the OR rule we must add these together to get a probability of 0.5.

Clearly, we must be careful when working with the OR and AND rules and make sure that the correct one is used at all times. Also, we need to remember that both of these rules may be used in the same question.

Example

A bag contains four red counters, five yellow and three blue. If, after picking out a counter, I note its colour and then replace it back into the bag, find the probabilities of the following:

1) Getting a blue counter first and then a red counter second.

2) Getting a yellow counter and a red counter in any order.

3) Getting a blue counter three times in a row.

1) Here we have a specific order of getting a blue counter which has probability  and then a red which has probability . Therefore, the AND rule says that we should multiply these separate probabilities to get 

2) Next, we can have a yellow counter and red but in any order. Firstly, the probability of getting a red and yellow counter is . Also we can have the two colours in any order so we can have yellow then red OR red then yellow. Both of these have the same probabilities since  is the same as . So the probability for either of the outcomes must be 

3) When finding the probability of three outcomes we use the same method as for any other number but we must obviously multiply three numbers instead of just two. The probability of getting a blue is  and we need to get a blue three times in a row, so the answer must be 

Conditional probability

Conditional probability, or dependent events, is the opposite of independent events. This means that the outcome of one event will be impacted by another. For example, if you pick a card from a standard deck, leave this out of the deck and then choose another, the second pick is a dependent event. This is because it is now impossible to choose the card that has already been removed. So the chances of picking certain cards have been affected by your first pick.

When working with conditional probability things can get a little confusing. This is because it may be hard to keep up with what events have happened and how they have an effect on others. The best thing to do is to use something called a tree diagram in these situations.

Outcomes in any order

When we are looking at outcomes that can happen in any order we must be very careful. The probability of getting two things one after the other, say a 2 and then 5 when rolling a dice, has the exact same probability of getting the two the other way around, so getting a 2 then 5 is just as likely as getting a 5 then 2.

The only thing that we must be careful of is that when something says that outcomes can occur in any order it means that we have more possibilities that can occur. Getting a 2 and 5 means we can get a 2 then 5 OR 5 then 2, so there are two options that can happen with the same probabilities.

When we have independent events that occur in any order we must first work out the probability of getting these in a particular order and then multiply this by the number of possible ways they can occur.

Example

What is the probability of getting two heads and a tail when flipping a coin three times?

Getting a tail and two heads means we must multiply the probabilities of  (for a tail) and  (for heads) three times. This gives us . However, there are a number of different ways we can get two heads and a tail. These are shown below:

HHT, THH, HTH

In each of the above situations we have the correct number of heads and tails and so these are all valid ways of achieving the outcome and must all have the same probability. So we can multiply the probability of getting two heads and a tail by the amount of different valid combinations. This then gives us