Pythagoras

Pythagoras was a Greek philosopher and mathematician who came up with one of the most used theories about right-angled triangles. He noticed that, for any right-angled triangle, there is a link between the side lengths. In order to use this theory we must first look at the different sides of a right-angled triangle.

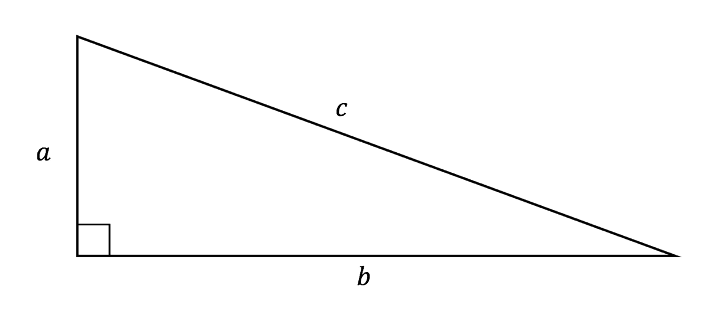
From the above we can see that the sides have been labelled as a, b and c. This is very common when working with right-angled triangles and the longest side (the one across from the right angle) should be labelled as c. The other two labels do not matter so can be either a or b. Using this we can use the theory of Pythagoras which tells us:

This means that, if we measure the three sides of a triangle, the two smaller sides squared will add together to give the longer side squared. This rule works for all right-angled triangles and will always be true.

Finding unknown sides

Since we now know about the Pythagoras rule, we can use this to solve various questions. If we have the length of two sides of a right-angled triangle, it is possible to work out the third.

With this knowledge we can work to find unknowns in diagrams as long as we have certain information. However, to do this we need to remember the rules of solving equations that we have learnt earlier in this course as well as how to deal with indices. Since the Pythagoras equation contains indices, we will need to use the square root function () on our calculators.

Example

Use Pythagoras to work out the side length of the following triangle:

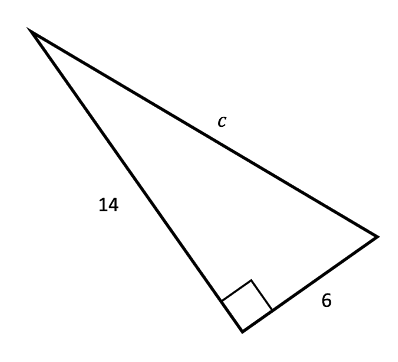
In this example we can see that a and b are 14 and 6. We can then put these into our Pythagoras equation to get:

Therefore, the side is equal to 15.23 to 2 decimal places. Here we can see that, using two side lengths, we have been able to work out a third for a right-angled triangle.