What is the quadratic formula?
Despite being a useful skill, it does take quite a bit of time to factorise an expression, then set each bracket to 0 and find the correct value of the unknown. This can be avoided if we make use of the quadratic formula which will be given to you in your exam. This formula will give the correct value for given any coefficients and is shown below:
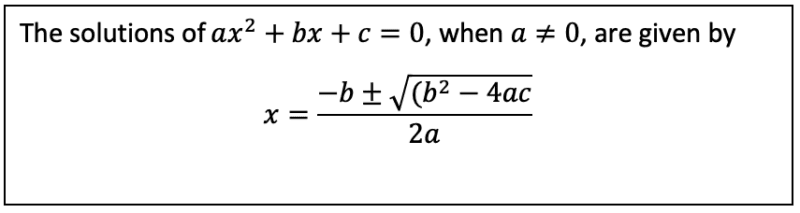
Since the equation will be given to you in your exam you will not need to learn it completely but just how to use it.
There are three different stages that you must apply when using the formula:
1) Identify the values of a, b and c.
2) Substitute these values into the formula and find the correct value for x.
3) Decide how many decimal places your answer should be given to.
Obviously, it will be easier if we split the formula up and work out smaller parts, as the entire thing is quite long to type into a calculator. As well as this it is worth noting that the use of ![]() will give us two possible results for x.
will give us two possible results for x.
Example
Use the quadratic formula to find the value of the unknown value in the following equations:
1) ![]()
2) ![]()
3) ![]()
1) Here we can allocate the values of a, b and c as 3, 7 and 3 respectively. Putting these into the quadratic formula we get ![]() which is then worked out on a calculator to find the values of x as
which is then worked out on a calculator to find the values of x as ![]() or
or ![]() .
.
2) Here we do the same process and find a, b and c as 4, 15 and 10. Inserting into the equation gives an answer of ![]() or
or ![]() to 3dp.
to 3dp.
3) Now we have the values as 1, ![]() and
and ![]() which gives us an answer of
which gives us an answer of ![]() or
or ![]()
One easier way to think of the quadratic formula is to split it up into two separate parts. So
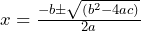
Becomes
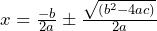
By splitting the denominator and writing this as above it becomes easier to work out two different parts and then work out one solution for x by adding the two, and the other solution by taking one from the other.
Note that the quadratic formula only works for equations up to ![]() and is not used for any higher powers than 2.
and is not used for any higher powers than 2.



