Rounding numbers

April 13, 2022

In this post

Why round numbers?

We use rounding of numbers to find a number near to the one we already have that is simpler. We can round numbers to any group but the most common are to the nearest whole, ten, hundred.

Usually you will be asked to round to the nearest whole number or ten.

Example

Round the following to the nearest ten:

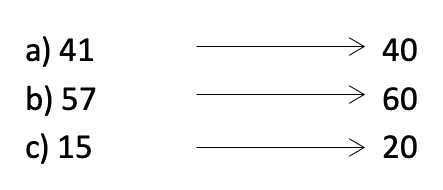
From above we can see that numbers can either be ‘rounded up’ if the nearest ten is larger than the original, or a number can be ‘rounded down’ if the nearest ten is less than the number given. If you are specifically told to ‘round up to the nearest…’ or ‘round down to the nearest…’ then you must find the next number larger or smaller than the given number.

As you will see from above, when we have the number 15, it is just as close to 10 as it is to 20. If we happen to be given a number that is midway between two possible answers then we must round the number up (unless the question specifically tells us to round down).

Rules for rounding:

Always round up or down according to the question but if you are asked to simply ‘round a number to the nearest…’ then do the following:

1) Look at the number which takes the place value which the question states. i.e. rounding 637 to the nearest 100, the digit in the hundreds is a 6.

2) Next we look at the number one place value below this number, so this is a 3 in our example.

3) If this number is a 4 or less, we round down and the answer is 600. Otherwise the number is rounded up and the answer would be 700.

Clearly in our example, 3 is less than 4 so we would round down.

If we consider the case where we have a number which has already been rounded, what could the original number have been?

If we have 500 which has been rounded to the nearest 100, then the original number could have been anything between 450 and 549. This is because the numbers 450-499 could be rounded up to 500. And the numbers 501-549 could have been rounded down to 500 and the number 500 would have simply remained the same.

Rounding decimals

In principle, rounding a decimal number is the same as rounding whole ones. However, instead of being asked to ‘round to the nearest hundredth or tenth’ you will usually be asked to ‘round to one, two or three decimal places’. Rounding to one decimal place is the same as rounding to the nearest tenth, two decimal places is to a hundredth, three to a thousandth etc.

Example

Round 3.6284 to the nearest two decimal places

The second decimal place is the 2, so we look at the next number to the right, which is an 8.

From this we know to round the second decimal place up to 3 so our answer is 3.63.

If we are asked to give a number to a certain amount of decimal places, we must always do this even if it means filling in zeros.

For example, 5.7 to three decimal places (3dp) is 5.700. The two zeros that we have added make no difference to the number but we now have an answer to three decimal places. This should always be done when asked to round a decimal.

Example

Round 5.8967 to 2dp.

This is equal to 5.90 when rounded and we must put our answer as this rather than 5.9.

Recurring decimals

We have already looked at how to convert between decimals and fractions, however, there are some fractions that can be very awkward to express as a decimal. The most obvious one being $\frac{1}{3}\$

To show $\frac{1}{3}\$ as a decimal we can write 0.33333, but this is only an approximation as we could really write an endless amount of 3’s in this decimal. Obviously, to save time we need some notation to show that we have many 3’s rather than writing them all out. This is where we use ‘recurring numbers’.

Recurring numbers literally just means ‘continuing indefinitely’ and are shown by placing a dot above the number. So 0.33333333333… is the same as $0.\dot{3}$ . We could also have numbers before the recurring number, so 0.12777777777 is the same as $0.12\dot{7}$ .

If we were to have a number which had a sequence that was recurring, then we show this by using two dots, one at the start and one at the end of the sequence. This then shows us that all the numbers in between are repeated.

For example,

0.81818181… $=0.\dot{8}\dot{1}$

0.658716587165871… $=0.\dot{6}587\dot{1}$

Whenever we see a recurring decimal it is a sign that the number can be replaced by an exact fraction. So, for example, $0.\dot{3}=\frac{1}{3}$ and $0.\dot{6}\dot{3}=\frac{7}{11}$