Very often people like to use a number line to give a visual idea of where numbers come in a sequence. This is done with the use of a number line as shown below.
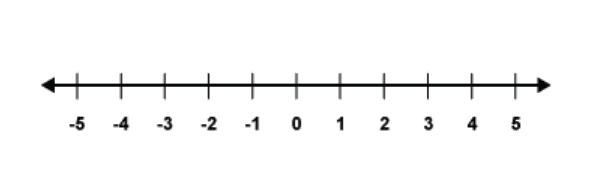
On a number line, the largest numbers extend to the right and the lower numbers (into the negatives) are towards the left. To find the gap between two numbers you can simply count the spaces between them on the number line.
There are not only the numbers shown above that exist, but there are also ones in between the integers. These are fractions and decimals.
Suppose we wanted to show on a number line all of the numbers that were above a certain value, say 1. This can be done as below.
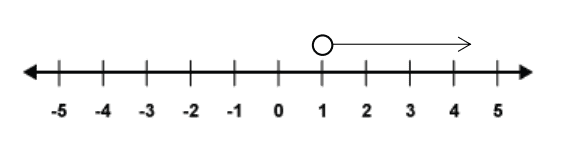
The use of a circle that is not shaded in tells us that 1 is not included; therefore, we have represented all of the numbers above but not included 1. This can be shown also by the inequality . Where x represents any number and is read as ‘![]() is greater than 1’.
is greater than 1’.
To show that we want to include 1, we can replace the circle for one which is filled in, like so:
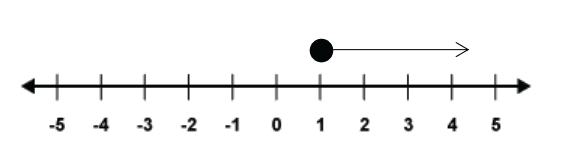
This then tells us that we are talking about the numbers more than 1, including 1 also. This can then be represented by the inequality . This is read as ‘![]() is greater than or equal to 1’.
is greater than or equal to 1’.
The same can be done for negative numbers:
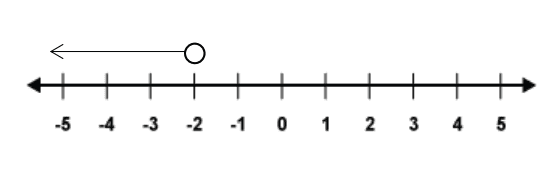
The number line above shows all the numbers below ![]() , but not including
, but not including ![]() . This is written as an inequality as and is said ‘
. This is written as an inequality as and is said ‘![]() is less than minus 2’. Next, we can show a situation where we may wish to include –2 in the numbers from the number line above. This would be written as the inequality , said ‘
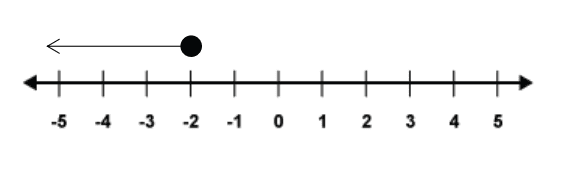
is less than minus 2’. Next, we can show a situation where we may wish to include –2 in the numbers from the number line above. This would be written as the inequality , said ‘![]() is less than or equal to minus 2’. We can represent this on a number line by using a filled in circle:
is less than or equal to minus 2’. We can represent this on a number line by using a filled in circle:
As well as showing numbers that are above or below a certain value we can use the same reasoning from above to show the numbers between two values. We call the two values, the upper and lower limits.
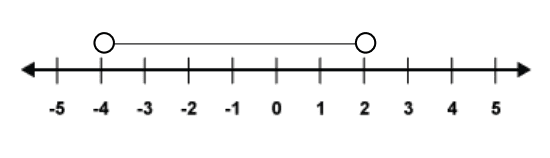
For example, say we wished to show the numbers between ![]() and
and ![]() , we could use the inequality . Which we would read as ‘
, we could use the inequality . Which we would read as ‘![]() is more than minus 4 but less than 2’.
is more than minus 4 but less than 2’.
This would then be represented on a number line by the following:
The same as above can be done to include the two limits also, by simply using a shaded circle as we have already seen. Therefore, ‘x is more than or equal to 1 and less than 5’ is shown as:
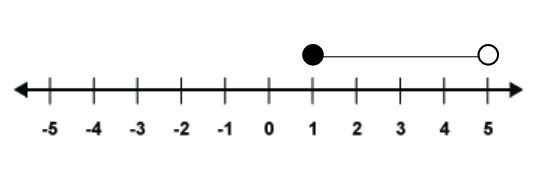
And as an inequality this would be .
Not all inequalities can work the same as this, for example if we wanted to combine the inequalities ![]() and
and ![]() we would get the inequality
we would get the inequality ![]() , which would be read as ‘x is more than or equal to 2 and less than –1’. Clearly there are no numbers that can suit this because it is impossible for a number to be both above or equal to 2 and less than minus one.
, which would be read as ‘x is more than or equal to 2 and less than –1’. Clearly there are no numbers that can suit this because it is impossible for a number to be both above or equal to 2 and less than minus one.



