In this post
Distance and length
We will begin this unit by getting to grips with some mathematical calculations on distance, time and speed. Distances are usually measured in units of centimetres and metres, but you may sometimes come across questions that require measurements in miles, hectares and other such distances. If this does happen, you should be told of the conversion rates between the two measurements, however, you need to know how to convert between centimetres, metres and other units directly related to these.
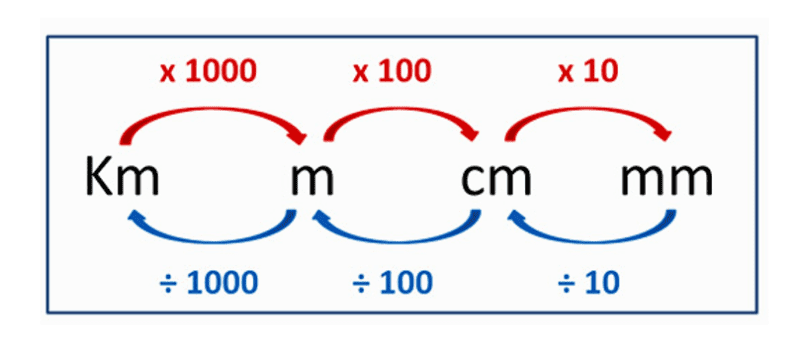
The picture above shows the conversion between the different metric measurements for length. When converting these units you should know that:
- there are 10 millimetres (mm) in a centimetre (cm)
- there are 100 centimetres in a metre (m)
- there are a 1000 metres in a kilometre (km)
Using these conversion rules, it is fairly simple to calculate the different amounts of each unit when required, as shown in the following examples.
Examples
Convert the following:
- 42 m into cm
To change m to cm we must multiply by 100.
To convert 42 m into cm we multiply 42 by 100 giving an answer of 42×100=4200 cm.
- 86 cm into mm
There are 10 mm in a cm, therefore 86 needs to be multiplied by 10 to get the answer of 860 mm.
- 3476 m into km
To convert directly from m into km we divide the value in m by 1000 to give us the value in km.
For example, 34761000 = 3.476 km
- 312 mm into m
Here we must convert 312 mm into cm first, which is done by dividing by 10 to 31.2 cm. Now we can convert this value for cm into metres by dividing by 100, so we get an answer of 0.312 m.
Similar methods can be used for converting between units for a range of values including capacity, time and speed.
Time
Time is something which is necessary to work out a relationship between distance and speed. If we said that someone travelled 5 km, we could not work out their average speed without first knowing the amount of time it took them to travel this distance.
In the exam questions it may sometimes be necessary to convert the time measurements given into different units.
Time is generally given in minutes and seconds. The conversion between different time measurements is fairly simple as there are the same number of seconds in a minute as there are minutes in an hour.
There are 60 seconds in a minute and 60 minutes in an hour. To convert hours into minutes, we must multiply the value by 60. To change minutes into seconds we also multiply the value by 60.
To convert seconds into minutes we divide by 60 and to convert minutes into hours we also divide by 60.
Example
Convert the following:
- 420 seconds into minutes
- 90 minutes into hours
- 2 hours into seconds
- a) Here we need to divide 420 by 60 to convert seconds into minutes. This gives an answer of 420÷60=7 minutes
- b) To convert minutes into hours we again divide by 60. The answer becomes 90 divided by 60 = 1.5 hours
- c) In this example, we firstly convert hours to minutes by multiplying the value by 60, giving an answer of 12 minutes. This value is then multiplied again by 60 to give us the answer in seconds. 12 x 60 = 720 seconds.
Adding and subtracting with time
Adding and subtracting time is fairly easy and works exactly the same as any other unit; however, we need to always remember that there are only 60 seconds in a minute and 60 minutes in an hour.
Example
A journey starts at 12.35 pm. Give the time when the journey finishes if the journey took a total of 3 hours 45 minutes. To do this we simply add the start time of the journey to the total time taken to complete the journey, making sure to add the hours and minutes separately:
| 12 hours 35 minutes |
| + 3 hours 45 minutes |
| = 15 hours 80 minutes |
As we know, there are only 60 minutes in one hour. This calculation gives a value in minutes which is higher than 60. Therefore, the value in minutes must be converted into hours and minutes, and the calculated value added to the total number of hours to give the journey end time. 80 minutes is equal to 1 hour 20 minutes. By adding 1 hour 20 minutes to the 15 hours, the journey end time becomes 16 hours 20 minutes or 16.20 pm.
Adding times is really only the same as adding any other numbers and the rules for ‘carrying’ numbers apply in the same way. The only difference is that this time we ‘carry’ a number when it is above 60 and not 100.
Example
A man finishes a race at 6.32 pm with a total time taken of 4 hours 47 minutes. At what time did he start the race?
In this example we subtract the total travel time taken from the finishing time of the race to work out the time at which he started the race, making sure to subtract the totals for the hours and minutes separately:
| 6 hours 32 minutes |
| – 4 hours 47 minutes |
| = 2 hours 15 minutes |
With this example we get a value for the minutes equal to -15. It is not possible to have -15 minutes, so we use the conversion rule of 60 minutes to an hour to convert this value into hours. A value of -15 means that we subtract 15 minutes from the total two hours giving an overall answer of 1 hour 45 minutes. Therefore, the man started the race at 1.45 pm.
If you need to brush up on long addition and subtraction and the idea of ‘carrying’ numbers, then we suggest that you do this before completing the exercises in the next part of the course.
Speed
The units that speed is quoted in always relate to the distance moved and the time taken. So we can give a value of 60 miles per hour, 80 strides per minute or any other combination of a distance and time.
The distance travelled is usually measured in metres, while time is usually measured in seconds. Therefore, as speed is equal to distance divided by time, speed is usually measured in metres per second (m/s).
In some exam questions the distance travelled may be quoted in cm or km and the time taken quoted in minutes or hours. This does not change the way in which you work out the unit of speed. The same equation for speed where speed equals distance divided by time is always used.
Average speed
To calculate the average speed we also use the same equation:
average speed = distance movedtime taken
Example
Calculate the average speed when each of the following distances was travelled:
- 40 miles in 5 hours
- 75 km in 5 days
- 80 m in 16 seconds
- Divide 40 miles by 5 hours, to give an average speed of 8 miles per hour
- Divide 75 km by 5 days, to give an average speed of 15 km per day
- Divide 80 m by 16 seconds to give an average speed of 5 metres per second
When we give a measurement of speed we must always also quote the units, which are calculated simply by doing the same calculations as with the numbers but with the units given. So for question a) we saw the answer was given in units of miles per hour, which is the same as miles/hour.
The unit of speed used is always equal to the unit of distance used divided by the unit of time used. To work out the relationship between distance, speed and time we can use the following formula triangle:
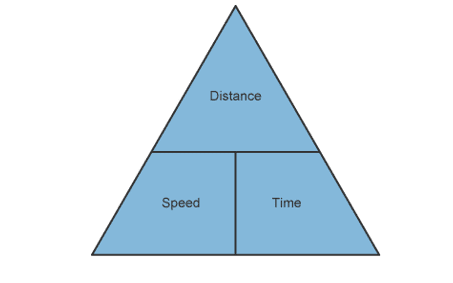
The formula triangle offers a visual aid to rearranging equations. To work out the correct equation using the triangle, you cover the desired value with your thumb and the equation is given by the relationship between the other two values based on their position in the triangle.
For example, to calculate speed, cover speed on the triangle to leave distance over time. The equation used to calculate speed is speed = distancetime. The diagram below summarises the equations used to calculate speed, distance and time. You must know these equations for the exam as they will not be provided for you.

The relationships between these equations allows you to calculate the value of any one of the three factors, as long as you are provided with the values of the other two as shown in the following examples:
Examples
- A dog runs 75 metres at a speed of 10 m/s. Calculate the time taken.
- A snail travels for 5 minutes at a speed of 0.1 m/s. Calculate the distance moved by the snail.
- Time taken = distance Time taken is calculated as:
75 m divided by 10 m/s = 7.5 s
- Distance moved = speed x time. This time you have to convert the time into seconds first. 5 mins x 60 = 300 seconds.
Distance moved is then calculated as: 0.1 m/s x 300 s = 30 metres.



