Gas laws

The way in which gases move and act is very intriguing, and there are certain properties and laws that you must understand for your examination. The forces of attraction between gas particles are very weak. This means that gas particles are able to move randomly, bumping into each other and the walls of whatever container they are in.

These constant collisions exert a force on the walls of the container. As we know, force is related to pressure so the more force the particles exert on the walls of the container, the more pressure they exert.

Molecules in a gas have random motion. They exert a force and a pressure on the walls of any container they are in. The pressure exerted by the gas particles in a container can be altered by changing either the area over which the collusions occur or the force with which the collisions occur. In this case, the force is provided by the collisions of particles themselves, so pressure is directly related to the number of particles we have in the container as well as the size of the container itself.

Boyle’s law

A scientist in the late 17^th century named Robert Boyle realised that air can be compressed. Boyle trapped some air in one container and was able to squeeze this same amount of air into a much smaller container. He conducted experiments where the temperature was kept constant but the pressure exerted on the gas was varied. Boyle measured the volume occupied by the gas at different pressures and his results are shown on the graph below:

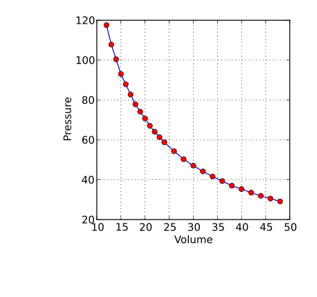
By examining his results, Boyle discovered that as he increased the pressure exerted on the gas, the volume taken up by the gas decreased. He discovered that this relationship was inversely proportional. When the pressure was doubled, the volume occupied halved. This inversely proportional relationship between pressure and volume is known as Boyle’s law.

Boyle’s law can be stated as:

“For a fixed amount of gas at a constant temperature, the pressure and volume are inversely proportional to one another”

Boyle’s law allows us to calculate the pressure (or volume) of one gas provided that the temperature is constant and that the gas’s volume (or pressure) is known, along with the pressure and volume of the second gas.

Imagine we have two containers filled with the same mass, and therefore the same number of particles of gas. Initially the pressure on both containers is equal and the volume taken up by the gas is equal. If the temperature is fixed and remains constant, any changes to the pressure applied would have an inverse effect on the volume occupied by the gas.

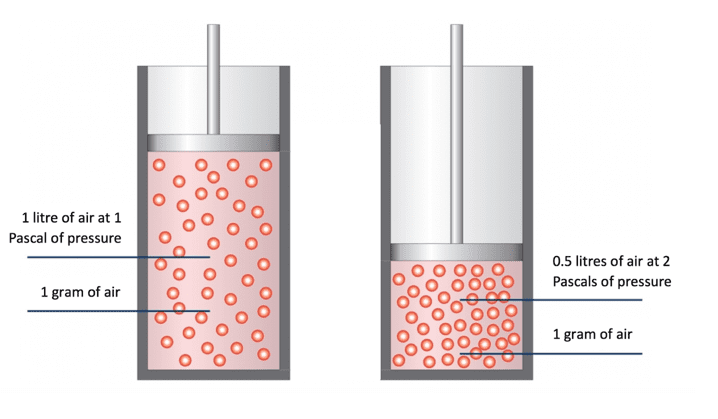
On the left we have 1 Pa of pressure added. The gas now takes up 1 litre of space. On the right we have doubled the pressure to 2 Pa and the gas now takes up 0.5 litres, exactly half the space from double the pressure.

The number of particles has not changed but they are now colliding with the walls of the container more often and with more force, therefore increasing the pressure. The equation used to represent the relationship between the pressure and volume of a fixed mass of gas at a constant temperature is:

In this equation,  p₁ is the pressure that is applied to a volume V₁ of gas. This must then be equal to a different pressure p₂ multiplied by a different volume V₂ of the gas. This equation follows Boyle’s law and assumes that the temperature and mass of the gas has been kept constant.

You should be able to use this equation to calculate the new pressure of a gas when the volume has been changed.

Example

A sealed syringe contains 0.94 of air at a pressure of 2.2 x 10³ Pa.

The plunger is pushed until the volume of trapped air decreases to 0.32 m₃.

Assuming that the temperature has remained constant, calculate the new pressure of the gas.

The pressure and volume of the gas before the change is known and the volume of the gas after the change is known. These values can be substituted into the equation:

The equation can then be rearranged to calculate a value for: