The difference of two squares

What is the difference of two squares?

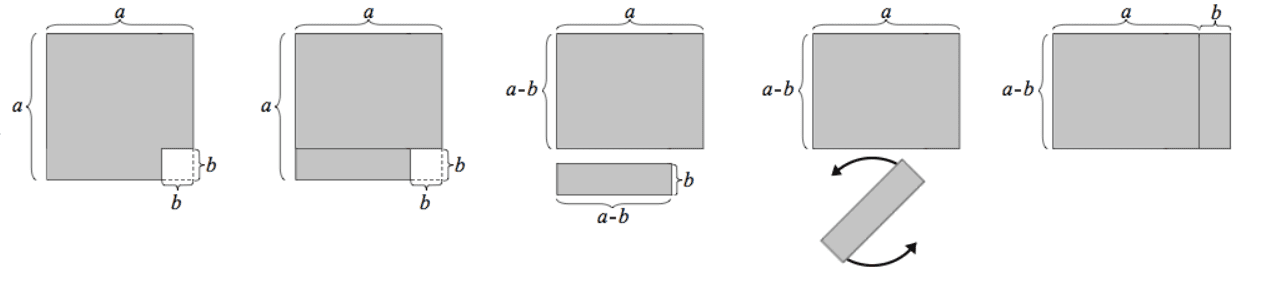
When we have an equation which contains only two parts it is often described as a ‘difference of two squares’. This can be summarised by the following:

When we expand the brackets we will see that the terms containing just a single will cancel out as we will have xa and ax. So when expanding the brackets we have:

We can easily factorise an equation like this so that we can have two brackets multiplied by finding the square root of each term. We can then place the square roots into our brackets for a with one being positive and the other negative.

Example

Factorise the following equations:

1) 

2) 

3) 

1) The square root of the two terms here (disregarding if they are positive or negative) are x and 2. This means that when factorising we have 

2) Using the same reasoning as in question 1 we get the answer of 

3) Here we need the square root of the term  which is . Therefore, we get the answer of 

As usual, the two brackets can be swapped with each other as the order which they are in does not have any significance .

Solving quadratics using the difference of two squares

When we can split an equation into two brackets by the difference of two squares we can use the same method of setting either bracket to 0 and then finding the unknown in each case. Therefore, if we had something like  then the solution for x would be when  or  making  or .

This can also be written as .

Perfect squares

Perfect squares are found when we have two brackets that are identical multiplied by one another. To expand the brackets the normal rules still apply but we will find that:

These rules are valid because if we have  which is the same as  collecting the  terms leads us to the answer of 

Similarly, if we have  then we have  (note that ). And now collecting the  terms we have the answer of 

Replacing the values of x and y with other numbers or unknown letters will still result in the same formula. Therefore, we can look to recognise expressions that, when factorised, will lead to perfect squares. These will clearly have a middle value (corresponding to  or ) that is two times the square root of the end value () times the square root of the first value (). Using this knowledge of perfect squares we can be quicker in identifying when they are involved in a question and can save time in finding the correct answer.

Example

Multiply out the brackets in the following:

1) 

2) 

1) By following the usual method of expanding brackets we find   Collecting the like terms and expanding then gives 

2) Again using the same method we get  which is the same as  which then equals 

Example

Identify which of the following expressions is a perfect square:

1) 

2) 

3) 

1) We need to identify which of the expressions will fit the equation for a perfect square . The first equation has which would make  so . This would then mean that the final term of  would need to be  but the term in the question is 16. So this is not the perfect square.

2) The second equation has  so . Then would equal 16. But in the question  so this is not the perfect square.

3) The final equation has  so again, . However, this time  matches the value that is in the given equation, therefore this is the correct answer and is the only equation that can be represented as a perfect square.