All about algebra

What is algebra?

Algebraic symbols are used to represent an unknown in many different types of equations. By putting in what is an unknown value, we can write out formulas that will depend and change in relation to a certain unknown value. Usually in algebra, an unknown term will be represented by a letter, but really the actual letter that is picked has no relevance and is only there to represent a value.

Why we need algebra

As already stated, algebra is used when we have an unknown. Therefore, we can use a letter to represent many different things and to answer different questions.

Example

How many drinks priced at £2 can I buy with:

a) £6

b) £10

c) £x

a) Clearly, we need to divide £6 by the price per drink of £2 to get an answer of 3 drinks.

b) Again, we divide the amount we have by the price per drink to get an answer of 5 drinks.

c) Here we do not know the amount of money that we have, however, we can use the unknown value of x and do the same as in parts a and b. So, the amount we can buy is drinks. We have now found a formula for working out the amount of drinks we can buy with any amount of money, represented by x.

Addition and subtraction in algebra

When adding or subtracting a number from an unknown value, we must use exactly the same rules as when we add or subtract with normal numbers. However, since we have an unknown value, we will not be able to get an answer and so we can simplify an expression but not give an answer exactly.

Example

Write down the following for a number denoted as n:

a) 10 more than n

b) 4 less than n

c) n plus 12 and minus 4

d) n plus the unknown value a

a) Here we get the simple answer of . This is because, without knowing a value for we cannot simplify any more.

b) This is equal to , which is clearly 4 less than , but again cannot be given exactly since n is unknown.

c) For this we get  which is the same as . This is because, despite not knowing the value of n, we can still simplify the other numbers to reduce the expression.

d) Here we are adding to unknown values, so the answer is . Since the value of n and a are both unknown, the expression cannot be simplified.

So, we now know that when adding and subtracting algebraic values, we cannot simplify any further than the algebra plus or minus a number. However, the known numbers, such as the natural numbers, can still be simplified in exactly the same way, they just cannot be combined with any algebraic symbol.

Multiplication and division in algebra

The rules for multiplication and division of algebraic terms are much the same as addition and subtraction. Any normal numbers in an expression that do not operate on an unknown can be calculated in the usual way. However, when operating on an algebraic value, we cannot get a number answer. Despite this, the rules for multiplication and division are still the same.

When multiplying two unknowns we can write , ab or ba. This is because when two algebraic values are seen as next to each other, it is implied that they are to be multiplied. Also, ab and ba are the exact same since multiplication is commutative, as we described in an earlier lesson on this course.

By dividing two unknowns we can simply replace the top and bottom of a fraction by the algebraic equation. Therefore a divided by b is the same as .

Example

Compute the following:

a) n multiplied by 6

b) n divided by 7 and multiplied by 3

c) n multiplied by p

d) n multiplied by 5 and divided by p

e) n multiplied by n

a) multiplied by 6 can be written as  which is just the same as

b) n divided by 7 is  which we must them multiply by 3 to get the answer of 

c) As explained earlier n multiplied by p will be the same as np or pn

d) n multiplied by 5 is . And we then must divide by p to get the answer 

e) Any number times by itself is a square. Therefore n multiplied by itself is equal to 

The rules for addition and subtraction of algebraic values can be used together with rules for multiplication and division. The only thing that must be observed is the BIDMAS rule that we looked at in module 1. By observing all of these rules, operations with algebra are simple and any mistakes will be avoided.

Substitution

Substitution is used when we find out the value for an unknown. Once we have a number which can be substituted into an algebraic expression we can work out a real number answer. For any of the expressions we have already looked at we could pick a certain value for the unknowns and then work out an answer without any algebraic symbols included.

For example, if we have  and are then told that  we can do the substitution for n, replacing it with 10. This would then give an answer of 

An unknown value can be replaced by a real number when the value is known in any type of equation we have already seen. Then we simply need to obey the BIDMAS rule to work out an answer.

Example

Calculate the following if x is equal to 4:

a) 

b) 

c) 

d) 

a) Substituting  gives the expression of

b) Substituting  gives the expression of 

c) when  is the same as 

d) Putting the value of 4 in for x we get  which is equal to 44

When substituting values in for unknowns we can have any number of algebraic constants. So if we had an expression with more than one value of x above, every time that an x appeared it should be replaced by the correct value. However, if the unknown value y appeared, this is not the same as x and so must only be substituted if its own value is known. Be careful to match the correct unknown to the substitution value!

Like terms

A great way to simplify an equation is by collecting ‘like terms’. This means that if there are multiple algebraic values, these can be added. However, different unknowns cannot, and so we look for parts that are ‘alike’, in that they use the same unknown.

Example

Simplify the following:

a) 

b) 

c) 

a) Here we have two different values of x which can be combined into one. Leaving the answer as 

b) With unknowns x and y we must combine values of the two separately. This gives us 

c) Using the same rules as before, we get the answer as 

Indices and fractions

The use of indices and fractions with algebra is done in exactly the same way as with ordinary numbers. By pretending that any letter is a number, and following the same rules that we have already seen in this course, you will be able to do different operations on algebraic functions.

Example

Simplify the following:

a) 

b) 

c)

a) Here we can add the powers, since this is the rule when multiplying indices. So we get an answer of 

b) Cancelling x from the top and bottom of a fraction is allowed, so this expression becomes just 

c) Here we can cancel an  and a  from the fraction (the same as cancelling by ) to get 

We can also have an unknown value as the indices in an expression such as . As with other operations involving algebra, the rules are the same as if the unknown was simply another number.

Use of brackets

Brackets are used in expressions to show multiplications between different algebraic values. When a number or letter is right before a bracket, that value is multiplied by all the different values in the bracket separately. This technique is known as ‘expanding brackets’.

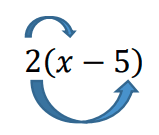
From above we can see that we get more than one calculation when this happens. Therefore, we must calculate both of the answers and then add them together. Above we would have  and  (keeping the correct sign is vital). This then gives an answer of 

Example

Expand the brackets in the following:

a) 

b) 

a) 7 multiplied by  gives  and 7 by  gives . Therefore, the answer is the addition of these two, 

b) x multiplied by  gives  and x by x is . So, the answer is the combination of those two, which is 

Do not forget that when two values are in brackets and next to each other, they must be multiplied. This means that  does not equal , the two brackets must be multiplied to give an answer of .

Example

Expand the following:

To do this we must multiply out the two brackets separately. Doing this as we have earlier we get . Now we can collect the ‘like terms’ in this to simplify further. The two unknowns that we have are x and y so when collecting these we get the answer as .

Key terms

Like terms – We collect like terms when the same unknown is used more than once; basically, we find a grand total of different operations on the same algebraic constant.

Expanding brackets – To expand a bracket we must multiply everything inside by the value on the outside.

Operations – All basic operations are done in exactly the same way as they are done on a normal number.