In this post
Geometry is a massive part of mathematics and deals with things like lines, angles and shapes. The basic ideas of geometry were founded many thousands of years ago in ancient times, but due to the real-world nature of geometry, they are as useful today as they were back then.
For this GCSE course, you will need to make use of a protractor, ruler and a pair of compasses. This is so that, when we get to later parts of the module, we can draw our own shapes.
Angles
One of the basics of geometry is the use of angles to draw shapes. An angle, as you will probably already know, is made by two straight lines that are connected at their tips. There are four main types of angles that we will look at.
Acute
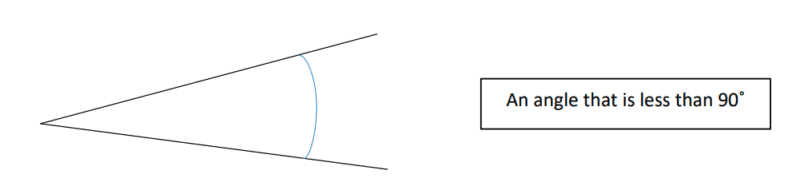
Right angle
Obtuse
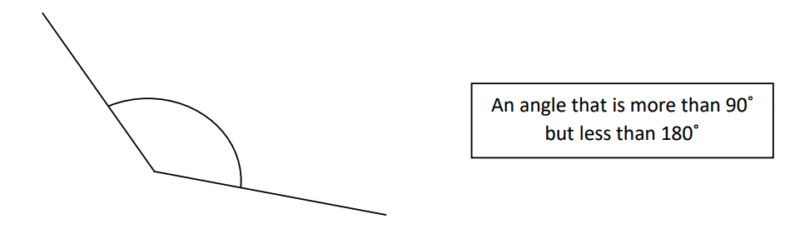
Reflex
| Name of angle | Definition |
|---|---|
| Acute |  |
| Right angle |  |
| Obtuse |  |
| Reflex |  |
Clearly, when an angle is exactly 180˚ or exactly 360˚ it does not fall into any of the above categories. This is because these angles will both just make a straight line. However, straight lines possess properties which are very useful when working with angles, something which we will look at next.
Straight line angles
The angle that is found on a straight line is 180˚. However, we can use this knowledge to work out other angles that are connected to a straight line.
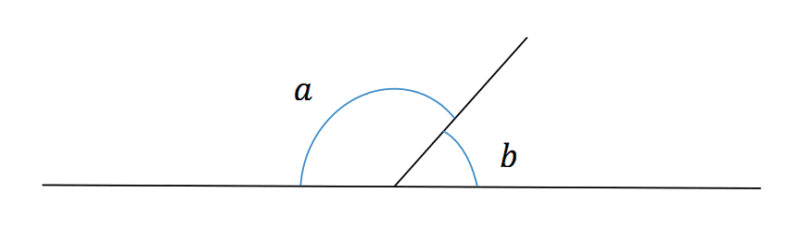
From the above diagram, since we know that the bottom line is a straight line and that the angle for a straight line is 180˚, we can say that angles a and b must add to 180˚. This is a very useful property of straight lines that we can use for calculating unknown angles.
Another use of straight lines for calculating angles is seen when we have two straight lines crossing and forming four angles, like below.
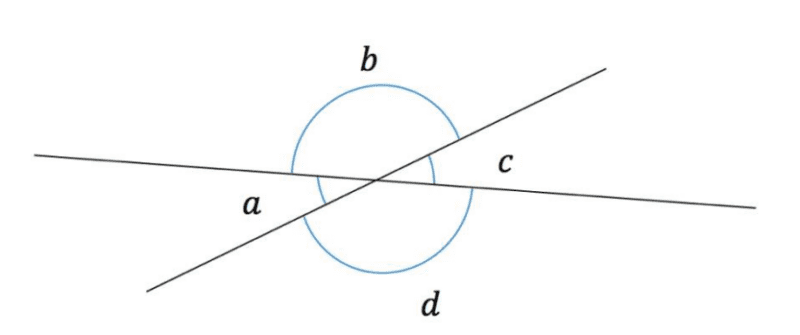
Since the full angle of a circle is equal to 360˚ we know that a, b, c and d must add up to 360˚. We can also say that angles a and c are equal; this is by a rule known as opposite angles. For any two angles that are opposite when two straight lines intersect (cross each other), their sizes are equal. Therefore, by the same reasoning we also know that angles a and b are equal.
Parallel lines
In geometry, a pair of lines are said to be parallel to each other if they are such that they will never cross even when extended for any length. This means that they will never form an angle between themselves and will always be the same distance away from each other. A good way to imagine this is to think of train tracks; the two tracks are always at the same distance from each other and never cross. This is shown below.
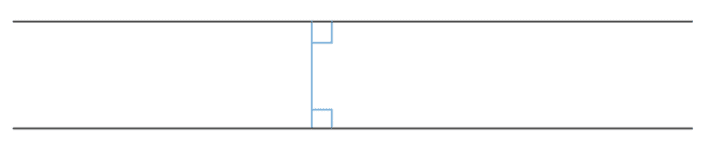
Shown above is the case where the parallel lines are perfectly horizontal and a vertical line cuts down through them. The angles formed by this are right angles as illustrated by the square corners.
When we have parallel lines that are intersected by another line (another line cuts through them like the example below) there are things we can say about the angles.
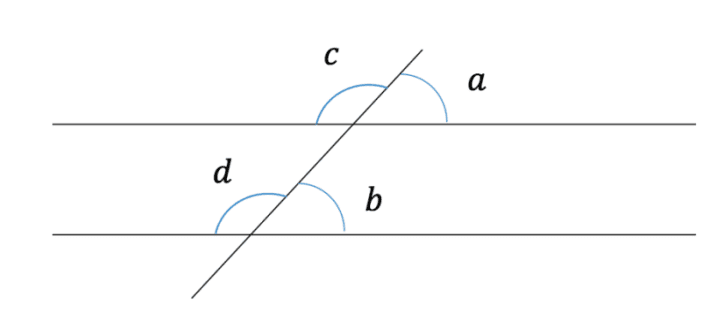
The angles a and b here are called corresponding angles and are equal. They are basically the same angle but for the opposing line of the pair of parallels. The same is true for the angles c and d.
As well as this, angles that are on a straight line can still be used here, so we also know that the angles a and c will add to 180˚. As do the angles b and d.
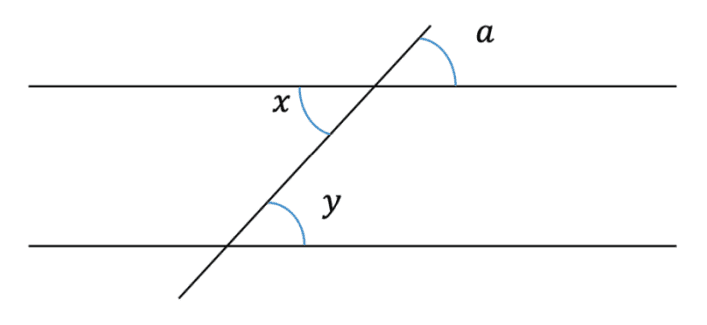
In the diagram above we have the angles x and y which are called alternate angles. If we consider the angle , we can say that this angle is equal to the angle x from the rules we have already seen of opposite angles. Angle a is also equal to the angle y due to them being corresponding angles. This then means that the angles x and y must be equal to each other. So we know that alternate angles are equal.
Example
Look at the diagram below and find the values of any unknown angles.
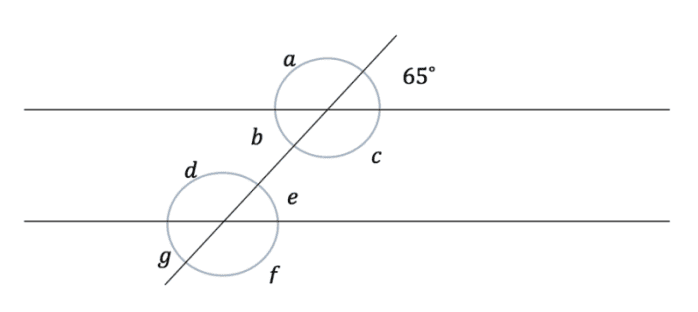
From the use of angles in a circle we can easily work out that angles a and c are equal, as are b and 
, e and g, and finally angles d and f are equal. Next, we can see that angles and are corresponding angles and so are equal, as are many others. When finding all of the equal angles we are left with:
and
Now, from knowing that angles in a straight line add up to 180˚, we can tell that angle 
. Therefore, we know that all the angles a, c, d and f are equal to 
. And we also know that angles b, e and g are equal to the angle .
So, from our knowledge of different angles with lines, we have worked out all eight of the angles in the problem when originally we only knew one!
Example
Find the missing angles in the following diagrams.
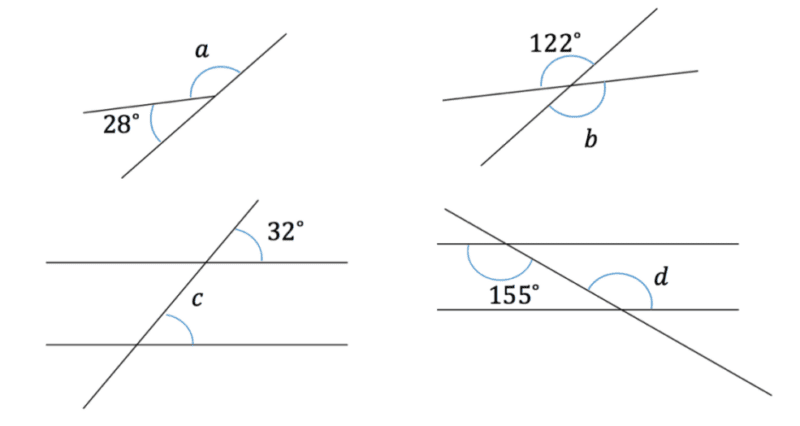
 | since angles in a straight line add up to  , so minus  gives the answer for a |
|---|---|
 | opposite angles make equal to its opposite of  |
 | corresponding angles being equal make c equal to  |
 | alternate angles being equal make d the same as the other angle of  |
