In this post
If we want to convert a decimal such as 
back to a fraction, we can use the idea of putting the recurring part of the decimal over 9. So the recurring part of is just the 3, so this is equal to 
.
For a decimal with more than one recurring number we must put the same amount of 9’s on the denominator of the fraction. For example, 
which can then be simplified accordingly.
If there are some digits before the recurring part of the decimal then we can get an answer by splitting the decimal into two parts and then converting them separately into fractions and adding the two fractions together.
For example, 
By representing 
as 
. we are able to convert to a fraction as stated above and then divide this by 10 after.
Significant figures and approximations
Another way that numbers can be rounded is if we want to round to a certain ‘significant figure’. To do this we must first understand the idea of a significant figure: the first significant figure is the first number from the left that is not a zero, the second significant figure is the next when going to the right and so on.
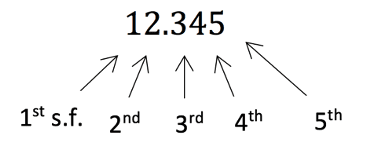
If we were asked to round the above number, 12.345, to a certain significant figure we would locate the s.f. stated and then look to the next number to the right; if this is 4 or less round down and if it is 5 or more then we round up.
The only time that zero is included as a significant figure is if it is not simply a placeholder. So the second s.f. in 0.028 is 8 but the second s.f. in 0.208 is a zero as there is a significant figure to the left.
So basically, a zero cannot be the first significant figure but it can be any other.
Example
Find the second significant figure of these numbers:
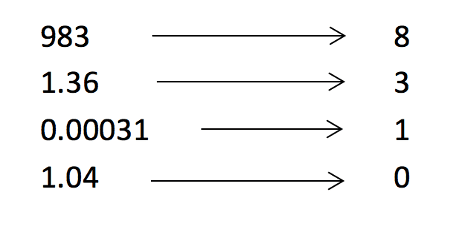
To round a number to a certain amount of significant figures we must leave an answer which has the correct amount of significant figures wanted.
In each of the examples above we have used the rules for significant figures which we have outlined above. All answers are then left with the correct amount of significant figures as stated in the question with zero being filled in as place value holders if needed.
Reciprocals
A reciprocal of a number is that number as the denominator of a fraction with 1 being the numerator, so the reciprocal of 8 is 
, 3 becomes 
and so on.
Therefore, the reciprocal of a number multiplied by the original is always equal to 1. The reciprocal of 12 
, 12 times equals 1.
Accuracy and errors
The majority of things in life do not fall into a certain category exactly. There are limits to how we can measure things and human errors can sometimes occur. Say we were to time a car journey as being 34 minutes. This time has actually been rounded to the nearest minute, so the time could have actually been anywhere between 33.5 and 34.5 minutes. These are called the limits which the measurement lies between.
The error when measuring the journey of 34 minutes is half a minute. This is because we could be half a minute below or above 34 minutes and, when rounded, this would still be our answer. Any further away than half a minute and we would have got a different answer to 34 minutes.
Example
Round each of these to two significant figures:
Upper and lower bounds
We can use upper and lower bounds to understand the accuracy of measurements that have been taken. When given a measurement that has been rounded, we must understand that there could be a certain error in this. By finding out the upper and lower bound we will know this level of error.
The lower bound is the lowest possible number that our measurement could be. For example, if we measure a length of wood to the nearest centimetre and find this is 18cm, the lower bound is 17.5cm as this is the smallest possible length the wood could be that still rounds to our measurement of 18cm. Similarly, the upper bound of this wood is 
cm as this is the highest possible value that can be rounded down to 18cm.
Often when working our upper and lower bounds we will round these boundaries themselves to the nearest whole logical choice. In the example above, we can say that the boundaries are 17.5cm and 18.5cm rather than using a recurring number.
