Powers of fractions

April 14, 2022

In this post

Fractions and powers

Sometimes we may need to find the answer to indices when the base is a fraction. To do this, the same rules of indices are used as before but we can also use some rules of fraction that we have already learnt.

Example

$(\frac{1}{2})^3=(\frac{1}{2}) \times(\frac{1}{2}) \times(\frac{1}{2})=(\frac{1 \times1 \times1 }{2 \times 2 \times2 }) =\frac{1}{8}$
To work this out we have had to use the rules of indices and then multiply the fraction the correct amount of times. Then, by using the fact that when multiplying fractions you can do the numerators and denominators separately, we get to the final answer.

Now we have a rule for getting the indices of fractions:

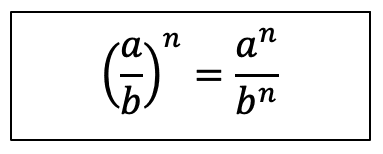
Where a, b and c could be any number. Again, do not worry if you do not understand this notation as it will become clearer when we move to the module on algebra.

Square and cube roots

Finding a square root of a number is basically the opposite of squaring something. So, if we were to square 5 we get 25, and then if we find the square root of 25, the answer is 5. This operation is shown by the symbol $\sqrt{x}$

A cube root is a number which must be cubed in order to get another. Therefore, the cube root of 8 is 2, since $2 \times2 \times2=8$ . So, we can write the cubed root of 8 as $\sqrt[3]{8}=2$ . This is the same symbol as square roots but with a small 3, which can be replaced with any other number to find the fourth root, fifth root etc. However, for this exam you will not need to work out anything that goes beyond a cube root.

These symbols should be clearly labelled on your calculator and you should refer to the instructions if you are unsure how to use them. We can also use this rule when faced with a problem that requires us to take a square or cubed root of a fraction. For example, if we need to work out the square root of $\frac{1}{16}$ :

\sqrt{\frac{1}{16}}= \frac{\sqrt{1}}{\sqrt{16}}=\frac{1}{4}

By using the rule for squaring fraction in reverse we can see that:

\sqrt{\frac{a}{b}}= \frac{\sqrt{a}}{\sqrt{b}}

Where a and b can be any number.

This rule also works for cube roots:

\sqrt[3]{\frac{a}{b}}= \frac{\sqrt[3]{a}}{\sqrt[3]{b}}

Example

Find the square root of $\frac{9}{25}$

\sqrt{\frac{9}{25}}= \frac{\sqrt{9}}{\sqrt{25}}=\frac{3}{5}

Find the square root of $\frac{27}{125}$

\sqrt[3]{\frac{27}{125}}= \frac{\sqrt[3]{27}}{\sqrt[3]{125}}=\frac{3}{5}

These calculations can easily be done on a calculator in the exam but it helps to know the method also.

Powers of fractions

In this post

Fractions and powers

Example

Square and cube roots

Example

Looking to get a GCSE?

Start your learning journey

Save your cart?