Quadrilaterals

April 7, 2022

In this post

Any four-sided shape falls into the category of being a quadrilateral. The only rule is that the four sides cannot be curved in any way: they must all be straight. The angles that are interior in any quadrilateral will always add up to $360^\circ$ . This is similar to how angles in any sized triangle will add to $180^\circ$ which we have already explored on this course.

To verify this fact we can simply look at any quadrilateral, such as the one below, and put a line through it that splits the shape into two distinct regions.

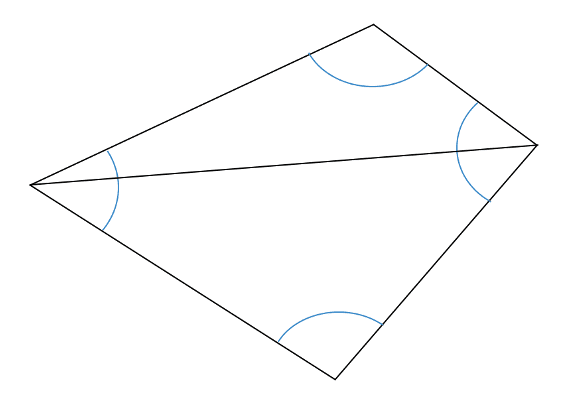
The quadrilateral has been split into two triangles, which must both have interior angles that add up to $180^\circ$ . Therefore, the quadrilateral, which is made of two triangles, must have interior angles that add to $2 \times180^\circ=360^\circ$ .

This same technique can be done for any quadrilateral, so we can conclude that all quadrilaterals have interior angles that add up to $360^\circ$ .

Types of quadrilaterals

There are many different types of quadrilateral which we will now look at and some of their properties will be explained.

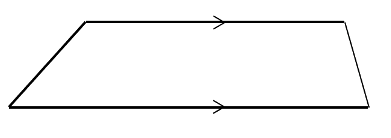
Trapezium

One pair of parallel sides.
Does not necessarily have any lines of symmetry (although some do).
Has no rotational symmetry.

Parallelogram

Has two pairs of parallel sides.
Each side in a parallelogram is parallel to the side that is opposite.
Rotational symmetry order 2.
No lines of symmetry.

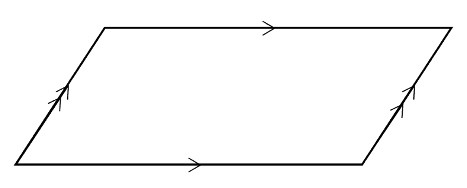
Other properties of a parallelogram:

Opposite angles are equal.
Adjacent angles add up to 180°.

Rhombus

A type of parallelogram that has four equal sides.
Therefore, a rhombus has all the same properties of a parallelogram as well as having two lines of symmetry.

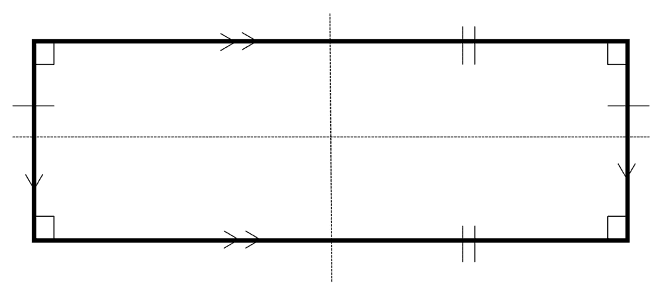
Rectangle

Two pairs of parallel lines.
Four right angles.
Two lines of symmetry.
Rotational symmetry order 2.

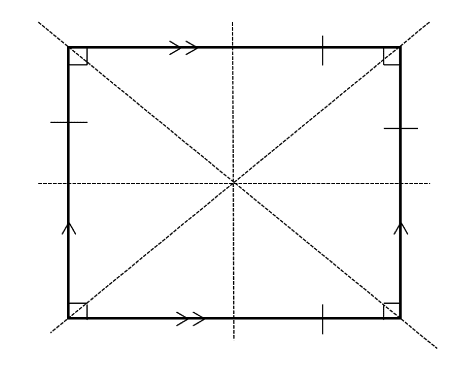
Square

Two pairs of parallel lines.
Four right angles.
Rotational symmetry order 4.
Four lines of symmetry.
Four sides of equal length.

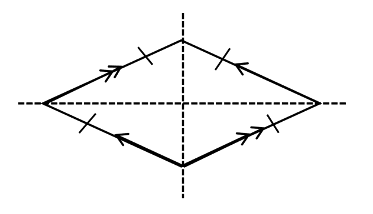
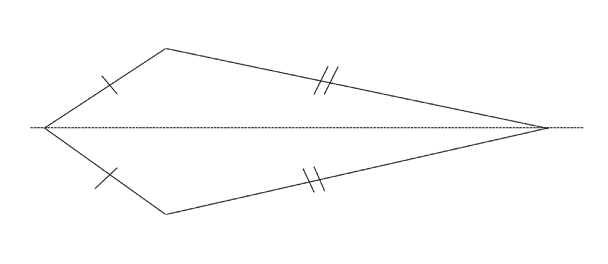
Kite

Two pairs of sides that are equal in length and parallel.
Equal sides are next to each other, not opposite.
One line of symmetry.
No rotational symmetry.

Example

Find the unknown angles and in the following diagram.

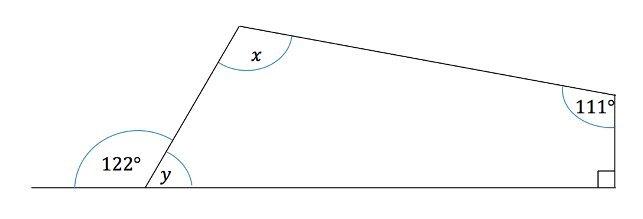
The angle y can be found using what we know of angles on a straight line. So it is equal to $180^\circ-122^\circ=58^\circ$ . Now angle x can be found by using the fact that angles in a quadrilateral add up to $360^\circ$ so therefore $x=101^\circ$ .

Polygons

A polygon is just a name for a shape which has all straight sides. This means that a triangle is a polygon with three sides and a quadrilateral is a polygon with four sides. Below is a list of some more names of polygons that you should try to remember.

Name	Number of sides
Pentagon	5
Hexagon	6
Heptagon	7
Octagon	8
Nonagon	9
Decagon	10
Dodecagon	12

Summing the interior angles of a polygon

The best method for summing the angles that are in any polygon is to choose any of the vertices and then draw lines to all the others from this particular vertex. This will then split the shape into a number of triangles which, as we have already seen, must have interior angles that sum to $180^\circ$ . Therefore, we can simply count the amount of triangles and multiply this by 180 to find the sum of interior angles for the polygon in question.

An example of this for a six-sided shape is shown below.

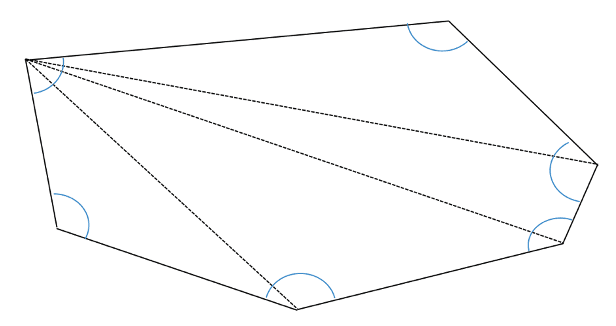
From this technique a rule can be found to find the sum of the interior angles for any polygon: we must take two from the number of sides and then multiply by $180^\circ$ .

If we call the number of sides that a polygon has n then for the sum of the interior angles we must calculate $(n-2) \times180^\circ$ .

Example

What do the interior angles of a nonagon add up to?

From the table seen previously we can see that a nonagon has nine sides, therefore using we can work out the equation $(9-2) \times180^\circ$ which gives the answer of $1260^\circ$ .

The sum of the exterior angles of a polygon

As the name suggests, the exterior angles to a polygon are on the outside of the shape. However, they are not simply $360^\circ$ minus the interior angle. To find the exterior angle we must extend the sides of the polygon and the angle that is made is the exterior one. This is shown below.

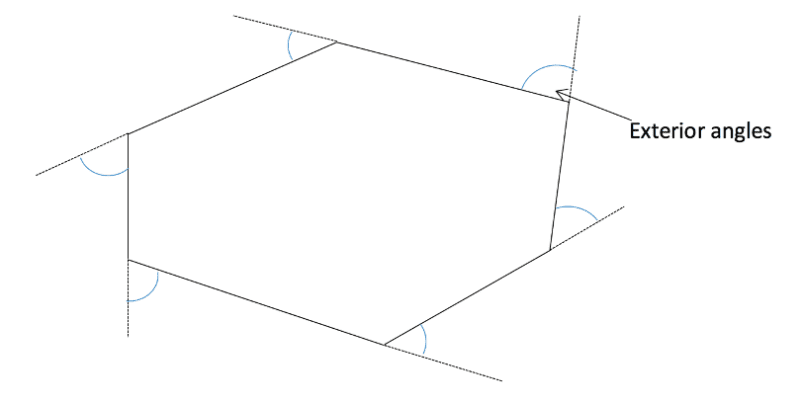
To sum these exterior angles we can picture ourselves standing on the edge of the shape at one vertex and walking around the outside back to where we started. At each corner we would have to turn the same amount as each individual exterior angle to carry on the edge of the shape. Once we were back to the start point we would have turned one full rotation in all. Therefore, we know that, for any polygon, the sum of the exterior angles is equal to $360^\circ$ .

Regular polygons

A regular polygon is a shape which has all of its sides the same length. Since all of the sides are the same length, all of the interior angles will be equal to each other also.

From this definition we can simply work out the size of each angle in a regular polygon by finding the sum of the interior angles and then dividing by the amount of sides which it has.

Example

Find the size of the interior angles of a regular hexagon.

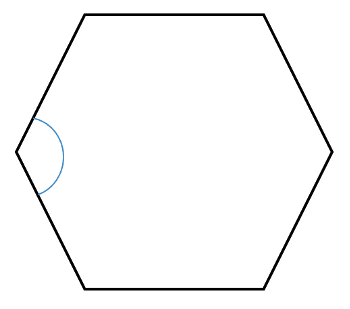
We wish to find the angle shown above which is equal to all the other interior angles. First we need to work out the sum of the interior angles for a hexagon, which has sides. Using the correct equation we have $(6-2) \times180^\circ=720^\circ$ . This sum of the interior angles is split up into six equal sized angles, therefore each of these must be $720^\circ \div6=120^\circ$ .

Example

Find the angles marked on the following diagram for a regular octagon.

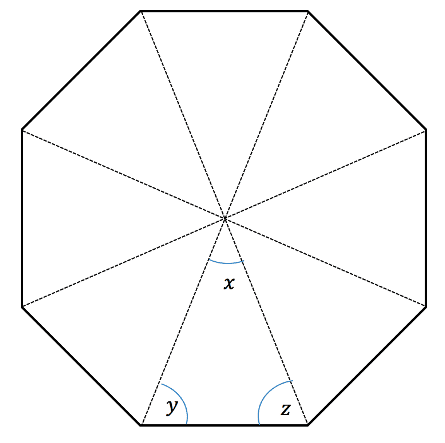
Angle x is simply one eighth of a full $360^\circ$ circle so this is easily calculated to be $45^\circ$ . The interior angle of the octagon must be equal to which are equal angles. So to find the size of y and z we must simply divide the interior angle by 2. Since we get the interior angle as $(8-2) \times180^\circ=1080^\circ$ Dividing this by 8 to find each angle in a regular octagon gives us $135^\circ$ . And finally, dividing by 2 to find the size of both y and z gives us $67.5^\circ$ .

Quadrilaterals

In this post

Types of quadrilaterals

Trapezium

Parallelogram

Rhombus

Rectangle

Square

Kite

Example

Polygons

Summing the interior angles of a polygon

Example

The sum of the exterior angles of a polygon

Regular polygons

Example

Example

Looking to get a GCSE?

Start your learning journey

Save your cart?