In this post
Square numbers
You may have noticed that some questions we have looked at involve multiplying a number by itself, like ![]() for example. This is known as ‘squaring a number’. Instead of writing
for example. This is known as ‘squaring a number’. Instead of writing ![]() we can write this as
we can write this as ![]() . The small two above the number is known as an indices and tells you how many times that you multiply a number by itself.
. The small two above the number is known as an indices and tells you how many times that you multiply a number by itself.
So ![]() tells you to multiply 2 lots of 4, and so we get
tells you to multiply 2 lots of 4, and so we get ![]() . The same can be said of
. The same can be said of ![]() being equal to
being equal to ![]() and so on.
and so on.
Really, any number that is by itself, say 9, can be written as ![]() since we have just one 9. However, this is not really necessary as we can see this by just writing 9, so an indices of 1 is never really used. But you should know that any number with an indices of 1 does nothing to the number.
since we have just one 9. However, this is not really necessary as we can see this by just writing 9, so an indices of 1 is never really used. But you should know that any number with an indices of 1 does nothing to the number.
A sequence of numbers which you should become familiar with is the square numbers. These are the numbers that you get when squaring 1, 2, 3, 4…
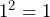
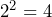
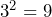
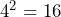
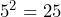
Now we understand the basics of squaring, we can ask, how can we get from a square number, say 16, back to the original number of 4?
This is done by use of the square root ![]() .
.
However, from the last section we know that ![]() since a negative multiplied by a negative is equal to a positive. So there are two numbers, 4 and
since a negative multiplied by a negative is equal to a positive. So there are two numbers, 4 and ![]() , which could have been multiplied by themselves to get to the number 16. Therefore, when we do the square root of a number, the answer can be either positive or negative. So, the answer to the square root of 16 is:
, which could have been multiplied by themselves to get to the number 16. Therefore, when we do the square root of a number, the answer can be either positive or negative. So, the answer to the square root of 16 is:
![]() or
or ![]()
This is read as ‘positive or negative 4’ or ‘plus or minus 4’.
So, all square roots have a positive OR negative answer and should always be written in the form as above.
Cube numbers
As we have just seen, the use of indices tells us how many times a number is multiplied by itself, and when we have 3 as the indices, this is known as ‘cubing’ a number. The first five cube numbers are:
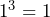
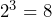
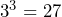
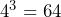
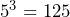
You should try to learn the square numbers up to 12 and the cube numbers up to 5 so that you do not have to use your calculator.



