In this post
Density
Density is a measurement of the amount of mass per volume of the substance.
It is vital that you understand the relationship between density, mass and volume for your examination. Without having a good knowledge of density and pressure it is not possible to fully understand the differences between the main three states of matter.
Solids have a very high density which means that they have a large mass over a small volume. The particles in liquids are more spaced out so liquids are less dense than solids. Liquids have a lower mass per volume. Gases have the lowest density of the three states of matter as the particles are very spaced out and there is less mass per unit of volume. This density is calculated using the following equation:
![\[ \text{Density} = \frac{mass}{volume} \]](https://online-learning-college.com/wp-content/ql-cache/quicklatex.com-9a1333238de1b04aa49269ea1df79090_l3.png "Rendered by QuickLaTeX.com")
You must know and be able to use this equation as it will not be provided in the exam.
The units used for density depend on the units for mass and volume. Density can either be measured in kg/m3 (kilograms per cubic metre) or g/cm3 (grams per cubic centimetre). The triangle shown in the diagram below can be used to work out how to rearrange the above equation to calculate mass or volume.
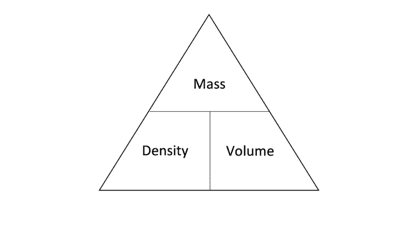
From these equations we know that the density of a substance can be determined by measuring its mass and volume. The volume of an object can be calculated by multiplying the length, width and height. The volume of an irregular object can be determined using a displacement can and a measuring cylinder.
Increasing and decreasing density
Since density is linked to mass and volume, any changes to these values will lead to a direct change in the density. For example, the are two ways in which the density can be increased. Firstly, the mass could be increased whilst the volume remains constant. This means that there is more mass in the same space. Secondly, the mass could be kept constant whilst the volume is decreased. This means that the same amount of matter takes up a smaller volume of space.
The density could also be decreased by reducing the mass or increasing the volume. Reducing the mass but keeping the volume constant reduces the amount of matter in the space. Increasing the volume with a constant mass means that the particles have more room to move and are not as close together.
Pressure, force and area
Pressure is defined as the amount of force exerted over a given area. Therefore, to calculate pressure, we need to know:
- The force or weight applied
- The area over which the force or weight acts
The area of any object is calculated by length by width. The unit commonly used for area is metres squared ().
Force is measured in Newtons (N) therefore pressure is measured in which are also known as pascals (Pa). For a force of 1 Newton acting on an area of 1 square metre, the pressure is 1 pascal.
The relationship between force, area and pressure is shown by the equation:
![\[ \text{Pressure} = \frac{Force}{Area} \]](https://online-learning-college.com/wp-content/ql-cache/quicklatex.com-d77c6ba309720a91c83536acef413b81_l3.png "Rendered by QuickLaTeX.com")
![\[ p = \frac{F}{A} \]](https://online-learning-college.com/wp-content/ql-cache/quicklatex.com-2f377f78a5a64f6a8662e02b07558666_l3.png "Rendered by QuickLaTeX.com")
Pressure is measured in pascals (Pa)
Force is measured in Newtons (N)
Area is measured in metres squared (m2)
You must know and be able to use this equation as it will not be provided in the exam.
Example
A force of 20 N acts over an area of 2.
Calculate the pressure.
![\[ \text{Pressure} = \frac{20 N}{2 m^2} \]](https://online-learning-college.com/wp-content/ql-cache/quicklatex.com-0201fe0c60c6d24d842e0232d6f0f117_l3.png "Rendered by QuickLaTeX.com")
![\[ \text{Pressure} = 10 Pa \]](https://online-learning-college.com/wp-content/ql-cache/quicklatex.com-fc59f708bb1d382bfe1d6b589e6c9e1e_l3.png "Rendered by QuickLaTeX.com")
The formula triangle which can be used to rearrange this equation and allow us to calculate force or area is shown below:
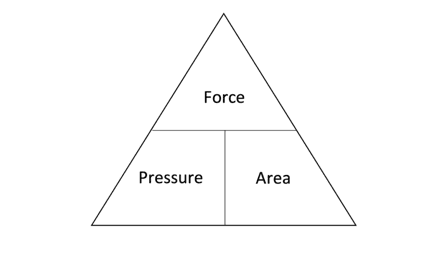
The equation used to calculate force is:
![\[ \text{Force} = \text{Pressure} \times \text{Area} \]](https://online-learning-college.com/wp-content/ql-cache/quicklatex.com-ec9ffa879a6897628549b5151db892cd_l3.png "Rendered by QuickLaTeX.com")
The equation used to calculate area is:
![\[ \text{Area} = \frac{Force}{Pressure} \]](https://online-learning-college.com/wp-content/ql-cache/quicklatex.com-8c5cbedb6ec9c7dbec2cbca524d5c4df_l3.png "Rendered by QuickLaTeX.com")
Increasing and decreasing pressure
Pressure can be increased or decreased by altering either the force applied or the area over which the force is applied. Force and pressure have a directly proportional relationship. As long as the area remains constant, as the force is increased, the pressure applied is also increased. If the force is increased and the area is kept constant, the pressure will also increase. If the force is decreased and the area remains constant, the pressure will decrease.
For example, imagine that two people are pressing a drawing pin into a wall and one pushes with more force than the other. The pin being pushed by the person who is pushing with more force will move further into the wall due to the higher amount of pressure being applied.
Pressure and area have an inversely proportional relationship. As long as the force applied remains constant, a decrease in the area over which the force is applied causes an increase in the pressure, and an increase in area causes a decrease in pressure.
For example, imagine if a person stood on your toe with the heel of a stiletto shoe and the heel of their trainer. The force would be equal for both types of footwear as it is the same person standing on your toe. However, the force is spread over a much smaller area for the stiletto heel than the trainer heel. The pressure exerted by the stiletto would therefore be much greater and it would be a lot more painful for you!
