The Beauty of Mathematics: Exploring GCSE Maths Theorems

January 26, 2025

Over the years, many young people have questioned the usefulness of maths. They may have asked their teachers or parents, “What use is maths in real life” or “Where will I use this in the future?” (usually algebra). At some point, they probably answered their own questions and realised that maths connects many aspects of their lives.

Maths plays a vital role in everyday life. You may use it when managing your finances, measuring ingredients for cooking or baking, calculating discounts during your weekly shops, and deciding what and how much materials you need for that DIY project. Even simple acts, such as being on time and dividing a pizza among friends, involve maths.

Some occupations require excellent maths skills for safety-critical jobs such as science, healthcare and engineering. For example, ensuring a bridge or building does not collapse, giving a patient the correct doses of medication and calculating fuel requirements for safe flights.

GCSE maths is a core subject, as it is widely recognised as being fundamental for young people’s futures. It helps them make sense of the world and enhances their problem-solving and critical-thinking skills. Most employers will ask for a good grade in GCSE maths, and those with excellent grades are likely to have better careers and overall success. Therefore, it is an invaluable subject in study, work, and overall life.

A vital aspect of the GCSE maths curriculum is mathematical theorems. Understanding these core principles will provide a foundation for advanced studies, enable students to grasp more complex concepts and see how different areas of maths are interconnected. It will help them develop essential skills that will aid in exam preparation and future careers and understand the relevance of maths in the real world.

Mathematics has practical applications but is also celebrated for its inherent elegance and beauty. For example, the Fibonacci sequence appears in nature in the arrangement of leaves and the spirals of shells. Additionally, the elegance of mathematical proofs, such as Pythagoras’ theorem, showcases how complex ideas can be distilled into concise, logical statements.

The beauty of mathematics lies in its simplicity, symmetry and ability to reveal patterns and connections that explain the world in which we live. The combination of practicality, beauty and elegance makes this fascinating discipline unique, and this blog post aims to showcase this.

What Are Mathematical Theorems?

Definition of a Theorem

A theorem is:

A mathematical statement that can be demonstrated (or proven) to be true.

Understanding the difference between a theorem, a hypothesis, and a proof is important:

A theorem – a proven statement or one that can be proven to be true, as defined above, using logical reasoning, a sequence of steps and previously established facts. They are fundamental truths in mathematics.
A hypothesis – an unproven statement or prediction believed to be true. It can be tested through experiments or observations. It is often the starting point of a problem to prove or disprove.
A proof – the logical process or argument of proving the truth of a theorem. It uses established mathematical principles, previously established theorems and axioms to show that a statement is true beyond doubt.
Axiom – a statement taken to be true (without requiring proof) to enable further reasoning.

Summary

Theorem – a proven statement.
Hypothesis – an unproven statement that can be tested.
Proof – the logical process of demonstrating a theorem’s truth.

The Role of Theorems in Mathematics

Theorems provide a solid foundation for more complex mathematical concepts in many ways. They:

Are proven using logical reasoning and structure, which is essential in advancing knowledge and developing new theories.
Often serve as stepping stones to more advanced concepts, as proving theorems introduces techniques used in more advanced mathematics.
Enhance problem-solving abilities and logical thinking, which can help tackle complex problems more effectively.
Are interconnected with other areas of mathematics, and many theorems are interrelated, i.e. understanding one can help understand others.
Can expand knowledge and skills in this subject, especially through the process of proving theorems.

Understanding and applying theorems is crucial for solving problems, especially in GCSE maths, as they:

Help build a structured understanding of mathematical concepts.
Allow for quick and accurate identification of solutions using proven principles and clear guidelines, leading to more efficient problem-solving.
Enhance analytical skills and the ability to break down complex problems.
Foster critical thinking and encourage questioning, analysis, reasoning and verification of solutions.
Provide a reliable way of approaching unfamiliar problems, which can boost confidence.

Theorems are essential tools in the problem-solver’s toolkit, ensuring clarity, efficiency and accuracy.

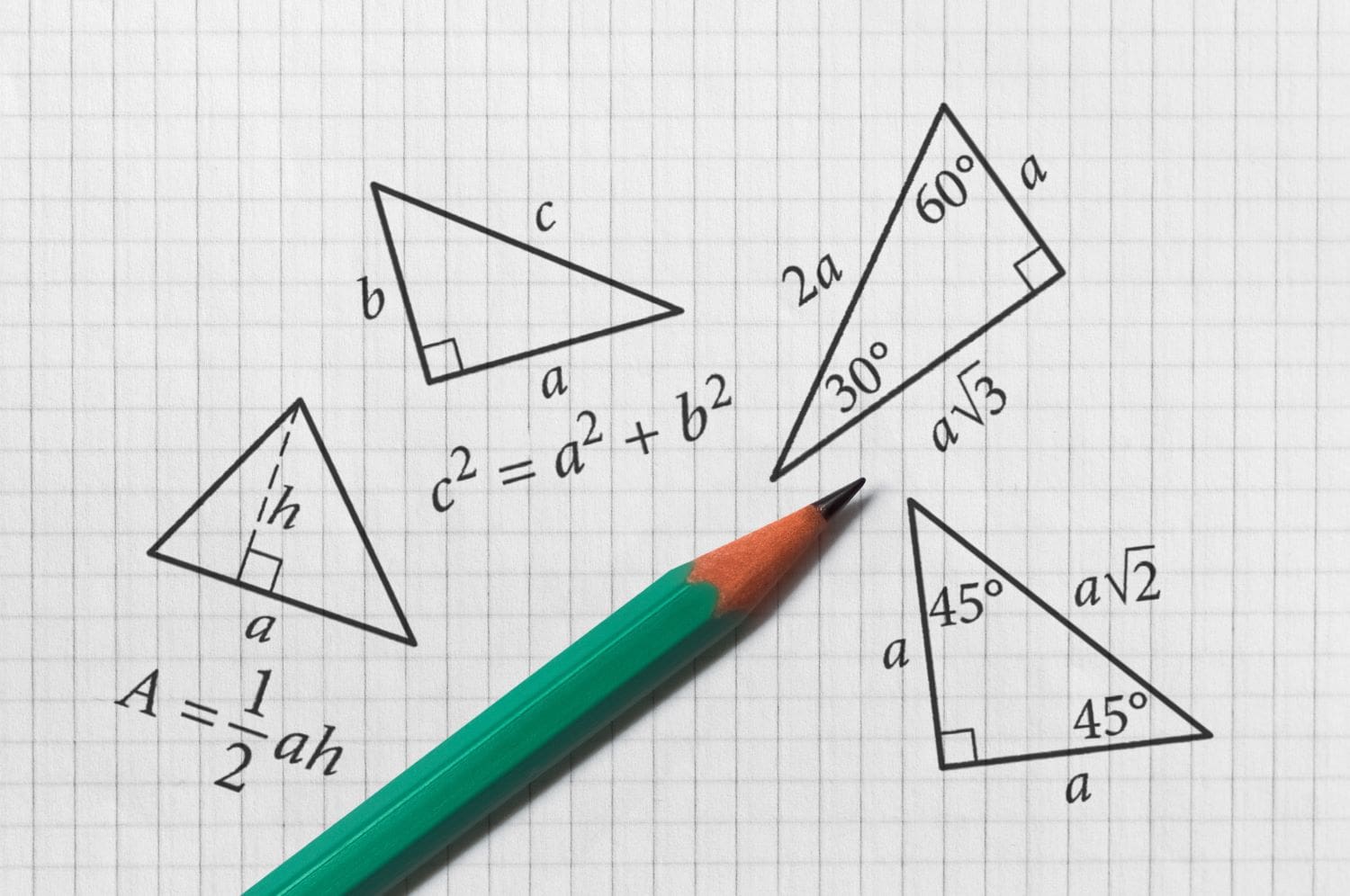
Key GCSE Maths Theorems

In GCSE maths, you will need to understand theorems, such as Pythagoras’ Theorem, the quadratic formula, trigonometric ratios, the angle sum theorem and circle theorems.

Pythagoras’ Theorem

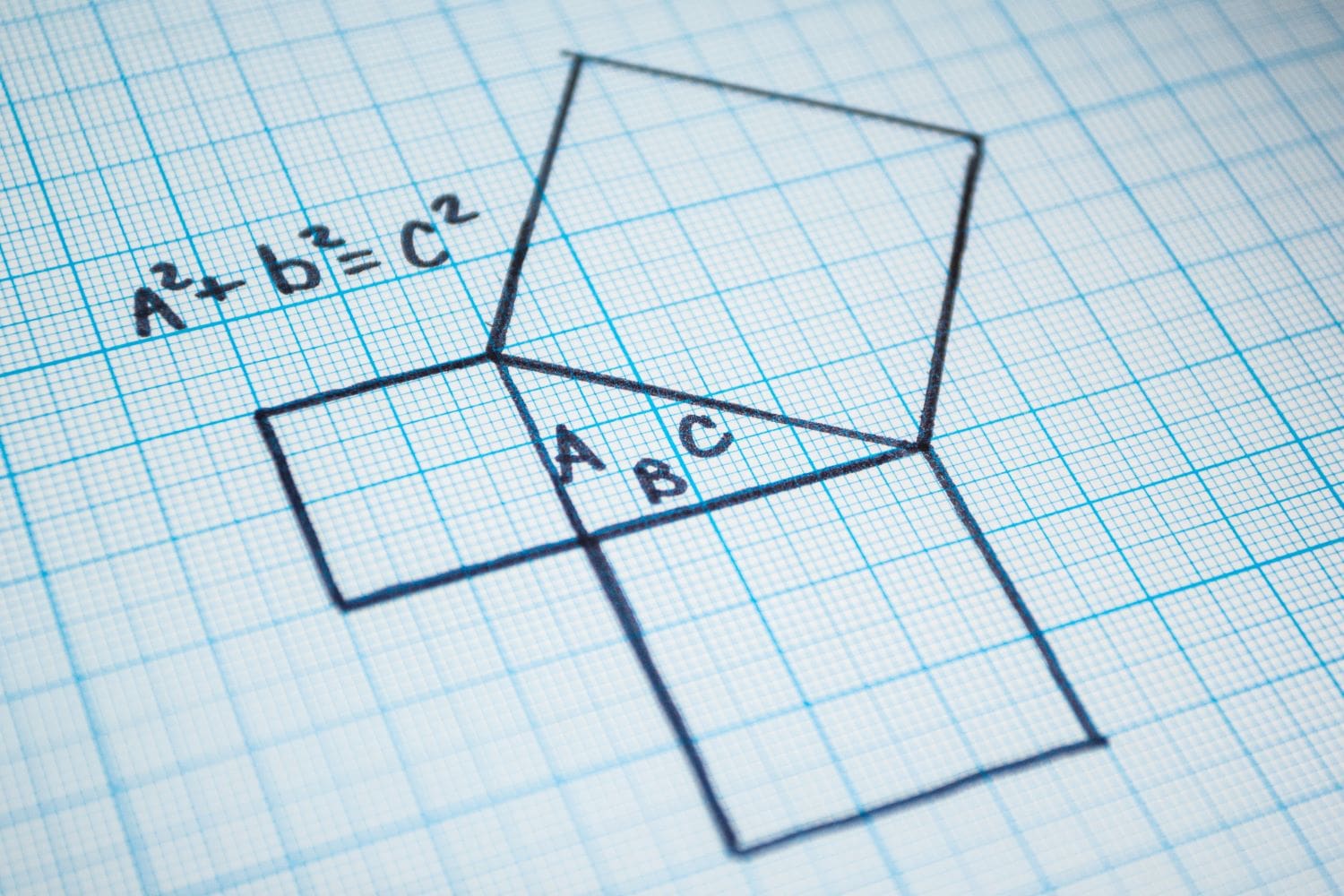
Pythagoras’ theorem is a fundamental principle in geometry and applies to right-angled triangles. It states that:

In a right-angled triangle, the square of the length of the hypotenuse (c²) is equal to the sum of the squares of the lengths/legs (a² + b²) of the other two sides.

It can be written as:

a² + b² = c².

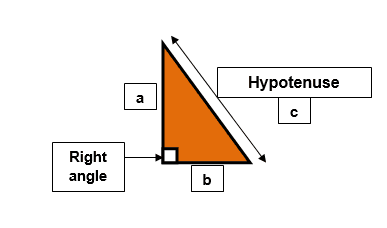
(c) is the length of the hypotenuse (the longest side opposite the right angle).
(a) and (b) are the other two sides (the lengths of the two legs with the shortest sides).

Here is an illustration to demonstrate this principle:

Here are some further points:

It only applies to right-angled triangles, i.e. with a 90-degree angle.
It can calculate the missing length of any side in a right-angled triangle.
It can be applied to solve 3-dimensional problems.

Pythagoras’ theorem has been used for thousands of years and was named after the Greek mathematician Pythagoras (c. 570–495 BCE). The theorem can also be traced back to several ancient civilisations. Babylonian clay tablets dating back to 1800 BCE and Egyptian 3-4-5 triangles used in pyramid construction show early knowledge of the theorem. Although the theorem is widely attributed to Pythagoras, it is clear that knowledge of the relationship between the sides of a right-angled triangle existed long before his time. Britannica has further information on the history here.

Pythagoras’ theorem is significant in geometry, as it aids in understanding the relationships between and within shapes and spaces, which is crucial for various practical and theoretical applications. It is also a foundational part of the maths curriculum, from primary to secondary school, and is often one of the first introductions students get to formal geometric proofs.

This theorem is applied frequently in the real world, for example:

Architecture and engineering – it is crucial in building design and construction, ensuring sound structures, appropriate proportions and accurate measurements.
Land surveying – it helps calculate distances and areas; crucial for determining property boundaries and land division, and creating maps.
Navigation – it is used in various navigation techniques, from mapping to GPS technology, aiding in precise location plotting, route planning and distance calculation.
Engineering – it is used when designing and constructing infrastructure like roads, bridges and tunnels, ensuring precise and safe construction.

The Quadratic Formula

A quadratic equation is a polynomial equation of the second degree involving a variable raised to the power of 2. The general form of a quadratic equation is:

ax² + bx + c = 0

(a) and (b) are coefficients (b is a coefficient of x and a is the coefficient of x²).
(c) is a constant.
(x) is the variable (unknown).
(a) cannot be equal to 0.
The variable gets squared like x².
The name quadratic comes from “quad” meaning square.
The ² is what makes the equation quadratic.
Constant – an unchanging number with a fixed value.
Coefficient – a factor that multiplies a variable in an expression and may contain both constants and variables.

Quadratic equations can be solved by:

Factorising.
Completing the square.
Graphing.
Using the quadratic formula.

The quadratic formula is used when solving an equation that cannot be factorised. It provides a method to find the solutions (or roots) of the quadratic equation and a way to solve for x in the equation ax² + bx + c = 0.

The formula is (you will need to learn this formula, as well as understanding how to use it for GCSE maths):

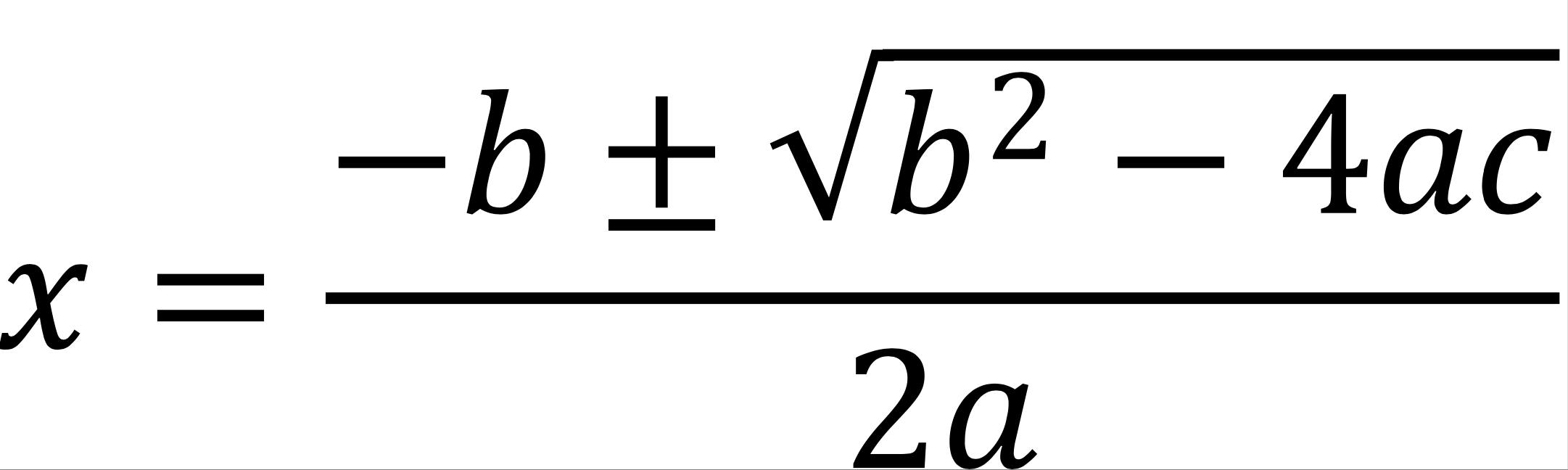
To use the formula:

Identify the values of a, b and c from the quadratic equation.
Substitute these values into the formula.
Perform calculations to find the values of x.

You will also need to understand differentiation, a technique to find the derivative of a function. The derivative represents the rate at which a function is changing at any given point. The quadratic formula is derived by completing the square on the general form of a quadratic equation. It requires the following steps:

Start with the standard form of a quadratic equation (ax² + bx + c = 0).
Divide by the coefficient of a.
Complete the square.
Take the square root of both sides.
Solve for 𝑥.

Maths is Fun has worked examples of the derivation of the quadratic formula here.

Functions – are mathematical rules with an input and an output.

This theorem is a powerful tool used across various fields such as physics, engineering, and economics. Here’s an example of how it’s applied in each of these areas:

Physics – often used to solve problems involving motion, e.g. the trajectory of a projectile, and in designing optics, such as solving equations related to focal length and curvature.
Engineering – used in various design and analysis tasks, e.g. when analysing the stress and strain on materials and structures.
Economics – used to find the maximum or minimum values of quadratic functions, which can represent profit, cost or revenue functions.

For further information, tips and tricks, see our other blog posts from our hub:

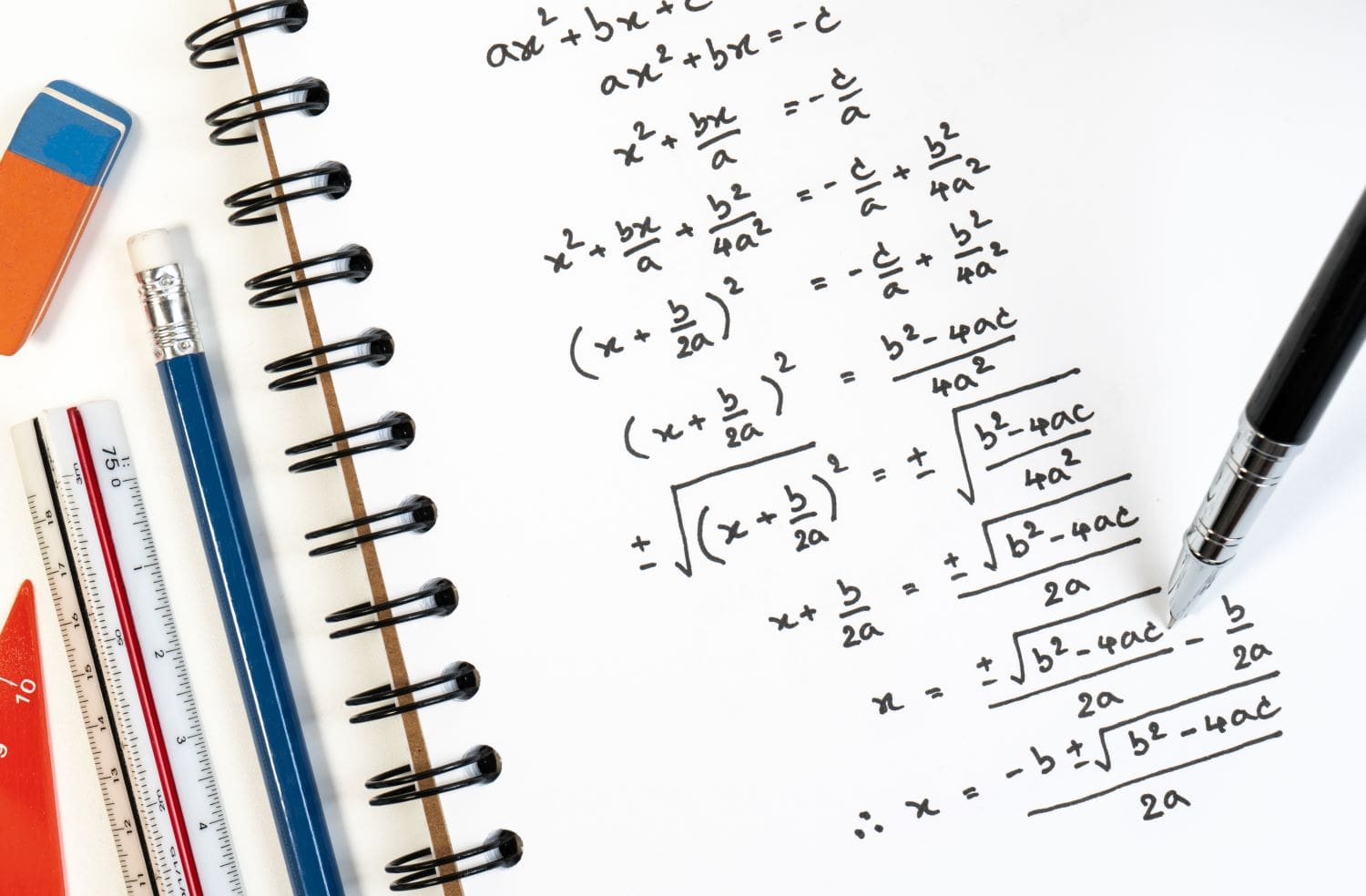
Trigonometric Ratios (Sine, Cosine, Tangent)

Trigonometry is all about the relationships between the angles and sides of triangles, particularly right-angled triangles. There are three basic trigonometric ratios (functions) to help navigate these relationships: sine (sin), cosine (cos) and tangent (tan).

Sine (sin)

The ratio of the length of the side opposite the angle to the length of the hypotenuse.
It is used to find the length of the side opposite the angle in a right-angled triangle.
Formula: sin(θ)=Opposite / Hypotenuse.

Cosine (cos)

The ratio of the length of the adjacent side to the length of the hypotenuse.
It is used to find the length of the side adjacent to the angle in a right-angled triangle.
Formula: cos(θ)=Adjacent / Hypotenuse.

Tangent (tan)

The ratio of the length of the opposite side to the length of the adjacent side.
It is used to find the length of the side opposite the angle relative to the side adjacent to the angle in a right-angled triangle.
Formula: tan(θ)=Opposite / Adjacent.

Some calculators have sin, cos and tan on them to make it easier, and you can put in the angle and press the appropriate button. However, you must still understand what they mean and how they work for GCSE maths.

A handy way to recall these ratios is SOH-CAH-TOA:

Sine = Opposite / Hypotenuse
Cosine = Adjacent / Hypotenuse
Tangent = Opposite / Adjacent

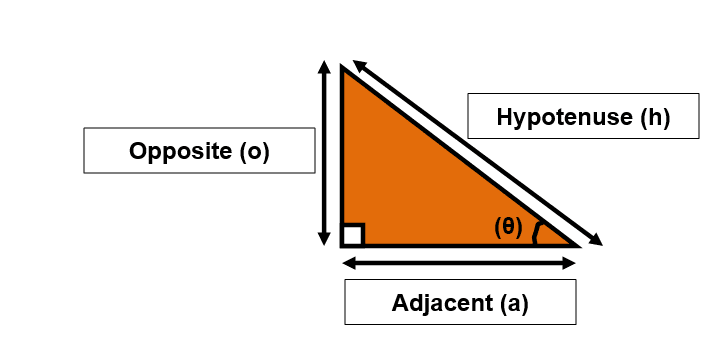
Hypotenuse (h) – the side opposite the right angle, and the longest side.
Opposite (o) – the side opposite the angle (θ).
Adjacent (a) – the side next to the angle (θ) and the right angle.

It is also important to be aware of reciprocal ratios, which are the inverses of the basic trigonometric ratios:

Cotangent (cot) – cot(θ) = 1 / tan(θ) = Adjacent / Opposite.
Secant (sec) – sec(θ) = 1 / cos(θ) = Hypotenuse / Adjacent.
Cosecant (cosec) – csc(θ) = 1 / sin(θ) = Hypotenuse / Opposite.

There are key relationships between these basic trigonometric ratios, for example:

Pythagorean identity

A rule that demonstrates the relationship between sine and cosine. No matter the angle, the squares of sine and cosine add up to 1.
It comes from the Pythagorean theorem: sin²(θ)+cos²(θ)=1.
This means that if you know the sine and cosine of an angle, you can always find the other one.

Quotient Identities

These identities relate the trigonometric functions to one another, e.g. tangent is simply the ratio of sine to cosine:
tan(θ) = sin(θ) / cos(θ).
cot(θ) = cos(θ) / sin(θ).

BBC Bitesize has a worked example of how Pythagoras’ theorem can be used to calculate the length of a side of the triangle here.

Trigonometric ratios are used in real-life applications, and here are some examples:

Designing structures – architects ensure stability in building structures by using sine, cosine and tangent to calculate angles. They also use these ratios for accurate design and measurement.

Calculating forces – engineers use trigonometric ratios to help them calculate forces in bridges, towers and buildings. They are crucial for determining stress and strain on materials.

Calculating heights and distances – trigonometry is used in many applications to calculate height and distance, for example:

Astronomers use it to calculate the distances between celestial bodies.
Geographers use it to create maps, especially for determining distances and elevations.
Pilots and sailors use it to plot courses, calculate distances and determine locations relative to coordinates.
Surveyors use it to accurately measure plots of land, ensuring property boundaries are correct.

The Angle Sum Theorem

The angle sum theorem is a fundamental concept in geometry, specifically related to triangles. It states that:

The sum of the interior angles of a triangle is always 180°, no matter the shape or size.

Triangle basics – a triangle is a polygon with three sides and three angles.
Interior angles – the angles inside the triangle are called interior angles.
Exterior angles – the angle formed outside the triangle if the side of a triangle is extended.

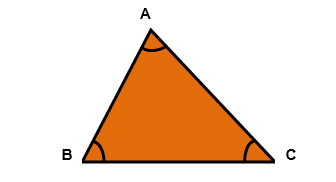
To help you understand this further:

Draw a triangle (as above).
The interior angles at vertices A, B, and C are denoted as:
- ∠A\angle A.
- ∠B\angle B.
- ∠C\angle C.
The formula of the angle sum theorem can be written as:

∠A + ∠B + ∠C = 180°

Understanding this theorem is crucial for solving various geometric problems and is a fundamental part of the GCSE Maths syllabus. BBC Bitesize has further information triangles and an example of a proof here.

It is also essential to understand the properties of different types of triangles (equilateral, isosceles, scalene and right-angled) for the following reasons:

It lays a foundation for geometry, understanding more complex shapes, and also for learning advanced topics like trigonometry.
Triangles have unique properties that can help students solve various geometric problems efficiently.
It helps prove and apply key theorems involving triangles, such as the Pythagoras’ theorem and further ones in mathematics.
It facilitates real-world problem-solving, as triangles are used in various practical fields.

This theorem has practical uses in various fields, including engineering and architecture, for example:

Engineering

Surveying – surveyors use the properties of triangles to measure distances and angles on the ground. The angle sum theorem is fundamental in these calculations.
Truss and frame design – engineers use triangular units for bridges and roofs in truss and frame design. Understanding the angles helps design trusses that can bear heavy loads without collapsing.
Structural design – engineers use triangular components to ensure stability and strength in structures like bridges, buildings and towers. Understanding the angle sum theorem allows them to calculate forces and stresses accurately.

Architecture

Building design – architects use triangles in various design elements to ensure the structural integrity of buildings. For example, roof designs use triangular shapes to distribute weight evenly.
Space optimisation – triangles can create efficient and aesthetically pleasing spaces. The angle sum theorem helps architects design these spaces accurately.
Historic structures – understanding triangle properties is crucial in preserving and renovating historical buildings, like the iconic spires and arches of cathedrals and historic houses.
Geodesic domes – these structures are made up of numerous interconnected triangles. Understanding the angles involved is crucial for designing stable and energy-efficient domes. Examples can be seen in projects like the Eden Project in Cornwall.

Circle Theorems

Circle theorems are the bedrock of geometry and often come up in GCSE maths. They are used in geometric proofs and to calculate angles. Some of the key circle theorems include:

Angle in a semi-circle – the angle in a semi-circle is always a right angle (90°).
Angle at the centre – the angle at the centre of a circle is twice the angle at the circumference. It can also be written as – the angle subtended by an arc at the centre is twice the angle subtended at the circumference.
Angles in the same segment – the angles in the same segment and standing on the same chord are always equal.
Cyclic quadrilateral – the opposite angles in a cyclic quadrilateral (a four-sided figure where all vertices touch the circle) always total 180°.
Alternate segment theorem – the angle between a tangent and a chord through the point of contact is equal to the angle in the alternate segment.
Tangent and radius – the angle between a tangent and a radius is always 90°.
Tangent of a circle – the tangents to a circle from the same point will always be equal length.
Chord of a circle – a line drawn from the centre to the mid-point of a chord is at 90° to the chord.
According to BBC Bitesize, subtend is an important word used in circle theorems, which means an angle created by an object at a given point.

Circle theorems have many applications, and here are a few examples:

Designing roundabouts – circle theorems help design roundabouts to ensure efficient traffic flow and safety. The tangents, arcs, radii and angles are calculated to maintain optimal curvature and visibility and ensure vehicles navigate smoothly. The angle at the centre theorem is used to determine the geometry of roundabouts, aiding in the planning of entry and exit points to facilitate efficient vehicle movement.
Sports – circle theorems are used in various sports, such as:
- Football – they are used to calculate the angles for goal kicks, passes and shots on target.
- Cricket – circle theorems help in fielding positions and predicting ball trajectories.
- Track design – athletic tracks are often designed using circle principles to ensure the even distribution of lanes and fair competition distances for races.
Arts – circle theorems are used in designing landmarks and buildings with circular features, ensuring aesthetic appeal and structural integrity. Artists also use these theorems to create visually appealing circular patterns and installations, often seen in public art projects.

Further details and worked examples of circle theorems are on:

The Elegance of Mathematical Proofs

Mathematical proofs are the epitome of elegance and precision in thought. They encapsulate complex ideas within clear and logical structures and unveil truths. Understanding and exploring proofs is essential for GCSE maths.

Understanding Mathematical Proofs

A mathematical proof uses logical reasoning and convincing arguments to demonstrate the truth of a mathematical statement beyond any doubt. It involves a step-by-step process to show why a theorem holds, which leads to a conclusion.

Proofs are essential in mathematics for many reasons:

They provide certainty and validate the truth when a mathematical statement is proven.
They lay a foundation for further proofs, as they build on existing theories.
They help clarify and understand why a particular statement is true and provide insights into mathematical concepts.
They ensure mathematical systems are consistent, meaning no contradictions arise within the set of established rules and theorems.
They allow mathematicians to communicate ideas precisely, as they are universal across cultures and languages.
They help solve problems methodically and logically, breaking them down into manageable steps.

There are various types of proofs, including:

Direct proof – involves starting with known facts, definitions and axioms and logically deducing by a straightforward series of logical steps the statement to prove.
Indirect proof (proof by contradiction) – involves assuming the opposite of what you want to prove is true and then showing that this assumption leads to a contradiction. This contradiction implies that the original statement must be true.
Proof by induction – involves proving a statement for a base case (proving the statement for the initial value) and then proving that if it is true for one case, it is true for the next case in a sequence.
Proof by contraposition – instead of proving the statement directly, prove that the contrapositive is true. If the statement is “if PP then QQ”, prove “if not QQ then not PP.
Proof by exhaustion – involves checking all possible cases for a statement to ensure it is true in every instance.

Contrapositive – a statement formed by negating and swapping the hypothesis and the conclusion of an original conditional statement.

Please see our other blog post for further information on hypotheses and proofs.

Exploring Proofs for GCSE Theorems

To succeed in GCSE maths, you will need to grasp simple proofs for key theorems, such as Pythagoras’ theorem.

Pythagoras’ theorem

Remember that Pythagoras’ theorem is:

In a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

a² + b² = c².

To prove Pythagoras’ theorem, you could:

1. Consider a right-angled triangle with sides a and b and hypotenuse c.

2. Construct a square with side length a + b, which contains the right-angled triangle repeated four times.

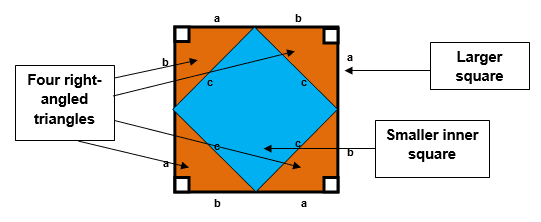
3. Calculate the area of the larger square: (a + b)²

4. Calculate the area using the smaller inner square (which has side length c) and the four right-angled triangles:

Total area = c² + 4 (½ab)

Simplify: Total area = c² + 2ab

5. Set the two area expressions equal:

(a + b)² = c² + 2ab

6. Expand the left side:

a² + 2ab + b² = c² + 2ab

7. Subtract 2ab from both sides:

a² + b² = c²

8. Conclusion:

We have proven that a² + b² = c²

BBC Bitesize has a video and a practical exercise on how to prove Pythagoras’ theorem here.

The angle sum of a triangle

Remember that the angle sum of a triangle theorem is:

The sum of the interior angles of a triangle is always 180°, no matter the shape or size.

To prove this theorem, you could:

Draw a triangle:

Let’s consider a triangle ABC with vertices A, B and C.

Draw a line parallel to one side:

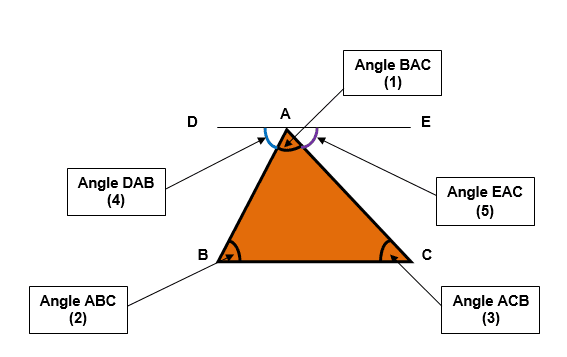
Draw a line DE parallel to the base BC, passing through the vertex A.
It forms two new angles at DAB (4) and EAC (5).

Use the parallel line to identify alternate interior angles:

Since line DE is parallel to BC, and AB is a transversal, we have:
Angle DAB (4) is equal to angle ABC (2). These are alternate interior angles.
Similarly, angle EAC (5) is equal to angle ACB (3). These are also alternate interior angles.

Identify the straight line angles:

The angles at point A, namely DAB (4), BAC (1), and EAC (5) lie on a straight line, and thus, add up to 180 degrees.

Combine the angles:

Notice that the angles DAB (which equals ABC), BAC and EAC (which equals ACB) combine to form the three angles of triangle ABC.
Therefore, angle ABC (2) + angle BAC (1) + angle ACB (3) = 180 degrees.

Conclusion:

By substituting specific angle measurements and using the properties of parallel lines and alternate interior angles, we’ve demonstrated that the sum of the interior angles in any triangle is always 180 degrees.

There is beauty and logic behind these proofs, as they are elegant, simple, and have a rigorous structure. They can explain complex ideas straightforwardly and insightfully, often unifying different areas of mathematics. They also use clear and logical steps to reveal truths and showcase inherent patterns and symmetries. They ensure conclusions are universally true and reliable, providing a solid foundation for further mathematical exploration and discovery.

The Real-World Applications of Maths Theorems

Mathematical theorems are found and applied in the real world, e.g. in nature, technology and engineering, and everyday problem-solving.

Mathematics in Nature

When you think of mathematical theorems, it is probably not in relation to nature. However, they appear frequently and here are some examples of how:

The Fibonacci sequence

Is a series of numbers where each number is the sum of the two preceding ones. It starts as 0, 1, 1, 2, 3, 5, 8, 13 and continues. For example:

0+1 = 1.
1+1 = 2.
1+2 = 3.
2+3 = 5.
3+5 = 8.
5+8 = 13.

What do you think the next number would be? It would be 8+13 =21.

This sequence is in the arrangement of leaves, flower petals or seed heads, the branching of trees, and even the spiral shells of certain molluscs. Example:

The seeds in a sunflower head are arranged in a spiral pattern.
These spirals can be observed to the left and right, and the number of spirals in each direction is typically consecutive Fibonacci numbers.
For instance, you might find 34 spirals going one way and 55 going the other.
BBC Bitesize has further information and an illustration of how this works here.

Symmetry

This refers to a situation when a shape or object looks the same after being transformed in some way, e.g. rotated, flipped, or shifted.
There are two types of symmetry: reflective and rotational.
Symmetry is in many aspects of nature, for example:
Reflective symmetry – if you split a shape equally by two, each other is a mirror image of the other, e.g. butterfly wings and some plant leaves.
Rotational symmetry – looks the same in more than one position when the shape is rotated about its centre (BBC Bitesize). Some examples in nature include snowflake structures, flower petals and starfish.
Fractals – essentially repeated patterns at different scales.
They are widely seen in nature, even in complex natural phenomena, such as lightning bolts, mountains and trees.
In smaller structures, they may be in snowflakes, your lungs and even broccoli. Perhaps it may make you see broccoli in a different light.
Right-angled triangles in nature – the Pythagorean theorem can be observed in natural structures like crystals, where right angles and triangular forms are common.

Technology and Engineering

Mathematical theorems underpin modern technology and drive innovation, for example:

Algorithms in software – when you chat with your friends and family online, algorithms use mathematical principles to compress, encrypt and transmit data. They also enable predictive modelling and decision-making processes in Artificial Intelligence (AI), powering recommendation systems and real-time analytics.
Game development – Pythagoras’ theorem helps calculate distances in 2D and 3D space, critical for graphics rendering and game development. Theorems are also important for creating realistic animations and virtual environments.
Structural engineering – engineers use theorems to select materials to build strong and stable buildings and structures, such as bridges and tunnels, that can withstand loads without collapsing. They help calculate forces, stresses, and loads on structures.

Everyday Problem-Solving

Theorems can also help solve everyday problems, and here are some practical examples:

Cooking and baking – theorems in algebra and arithmetic can help you understand proportions and conversions and accurately adjust ingredients. For example, if you have a recipe for four people and need to cook for six, ratios can help you scale up the ingredients correctly.
DIY projects – theorems relating to geometry can help with various DIY tasks, such as measuring spaces for furniture and calculating the amount of paint needed for a room. Pythagoras’ theorem can help to precisely measure an area for laying tiles to ensure everything fits perfectly or find the length of a diagonal wall or the correct length of a ladder needed to reach a certain height.
Financial calculations and decisions – theorems can help calculate discounts and interest rates on loans and risk assess various financial investment options. Theorems in economics and statistics help in making informed financial decisions. Theorems in algebra can help manage a budget, as it often requires solving for unknown.
Navigation – when trying to find the shortest path between two points, like navigating through a city, Pythagoras’ theorem can help determine the straight-line distance. Theorems in algebra and geometry can help calculate travel times and distances when planning a trip, considering factors like speed and time.

These examples show how maths theorems are not just academic concepts, but practical tools that help solve real-world problems. They provide a foundation for critical thinking and decision-making that can enhance various aspects of everyday life. BBC Bitesize has some questions on applying Pythagoras’ theorem in real life here.

Why Understanding Theorems Is Crucial for GCSE Success

Understanding theorems is important, as they play a vital role in GCSE maths exams and build a strong foundation for studying this subject at a more advanced level.

The Role of Theorems in Exams

In GCSE maths exams, you will have various questions that assess your understanding and application of theorems and their relationships. Theorems may be tested in the following ways:

Calculation questions – you may be asked to apply theorems to calculate unknown angles or lengths.

Short answer questions – you may need to solve a problem using a specific theorem, e.g.:

Use Pythagoras’ theorem to find the length of a side in a right-angled triangle.
Apply trigonometric ratios to find missing angles or sides in a triangle.

Proof questions – you may be asked to prove a given statement using theorems, e.g. proving that the angle in a semi-circle is 90° using circle theorems. They may require you to write out a proof or demonstrate your reasoning step-by-step.

Multiple-choice questions – you may have multiple-choice questions where you must choose the correct theorem that applies to a given scenario, e.g. identify which circle theorem applies to a given diagram. They may also ask you to select the correct calculation based on a theorem.

Diagram-based questions – you could be asked to label diagrams and draw graphs or plot points to demonstrate your understanding of theorems in a visual context.

Applied problems – you may be given real-world problems where you need to use mathematical theorems to solve practical issues, e.g. finding the height of a tree using trigonometry or how far the base of a ladder is from the wall by applying Pythagoras’ theorem.

Here are some tips for mastering theorem-based questions:

Understand all theorems.

It goes without saying that answering theorem-based questions requires a solid understanding of the core principles behind each theorem.
Understand how they work and their proofs and derivations. Do not just remember formulae.
Use some flashcards with theorems, formulae and their applications for quick revision.
Create acronyms to remember key concepts and theorems.

Work on proofs.

Break down proofs into clear, logical steps and understand why each step is necessary, which will help recall during exams.
Also, regularly practice writing out full proofs.

Practice past GCSE papers.

This is fundamental to your success and will familiarise you with the format and types of questions that will be asked in your exams. Make sure you:
Use past papers from your exam board, e.g. AQA, Edexcel, Eduqas, OCR, WJEC, etc.
Practice under mock exam conditions, e.g. time yourself and find a quiet location.
Practice different types of theorem-based questions, and do not just stick to one type.
Check your answers against marking schemes to see where you do well and the areas that need improvement.
Use the examiner reports to see what examiners look for and their comments.

Use diagrams.

When you face geometric problems, draw clear and labelled diagrams.
Visualising the problem can make it easier to apply theorems and identify relationships.
Do not forget to annotate your diagrams with known values and relationships.

Use various problem-solving strategies.

Quickly note down what is given in the problem and what you need to find.
Present your solutions in a clear and logical manner to help examiners follow your reasoning and increase your chances of earning full marks.
Always double-check your calculations and reasoning to avoid careless mistakes.

Stay organised.

Keep your notes well-organised and categorise them by topics to make revision easier.
Create summary sheets of key theorems and formulas for quick revision before exams.

Remain calm and confident.

Proper preparation for the exams and effective revision will help you feel more confident during the exams.
If you get stuck on a question, do not panic and stay calm.
Breathe, take a deep breath and re-read the question.
If you are really struggling, move on to another question and come back to it later.

Always seek help from your teachers, parents or tutor if you are stuck. There are also online resources, such as tutorials, videos and forums to get different perspectives and explanations.

Here are some tips for mastering theorem-based questions:

Building a Strong Mathematical Foundation

Theorems lay the foundation for advanced mathematical studies and are important as they will:

Teach you to construct rigorous arguments and avoid logical fallacies.
Enable you to connect different concepts, which can lead to a deeper comprehension of the subject as a whole.
Build your confidence and prepare you for complex topics in higher education when you master these theorems and various proof techniques early.
Help in other fields, like physics, engineering, computer science and economics, that use theorems.
Help you boost logical thinking and problem-solving skills by:
Enabling you to think in a structured and methodical way, as you will need to understand their conditions, hypotheses and conclusions.
Teaching you to construct solid arguments and enhance your logical reasoning abilities using various techniques and methods.Helping you to recognise patterns, see connections and apply known results to new problems.Enhancing your analytical skills, as you will learn to break down complex problems into smaller, more manageable parts and address each part systematically.
Helping you solve problems creatively, think outside the box and consider various ways to identify solutions.

Overall, theorems are crucial for understanding and advancing in higher-level mathematics. They can also be invaluable in other areas of study, work and life.

Mathematical theorems have stood the test of time and are used in every aspect of our lives, from education and careers to everyday problem-solving. They are also frequently in nature when we look at a flower, marvel at a magnificent structure or try to get to grips with a DIY project. They not only advance our understanding but also reveal the intrinsic beauty and order in the universe.

Conclusion

GCSE maths requires knowledge and understanding of key mathematical theorems, such as Pythagoras’ theorem, the quadratic formula, trigonometric ratios, the angle sum theorem, and circle theorems. These theorems form the backbone of mathematics. They are crucial not only for solving geometric and algebraic problems but also for developing logical thinking and problem-solving skills. They are essential in grasping more advanced mathematical concepts and their real-life applications.

There are many reasons to love mathematics and appreciate its elegance and practicality. It can uncover beauty, reveal patterns and structures and inspire wonder with discovering solutions and understanding complex concepts. It is a universal language that transcends cultural and language barriers and is useful in everyday life and various careers. It is also important for innovation, from technology to medicine, and is the backbone of advancements that improve our world.

This blog post, although detailed, has only touched the surface surrounding these fascinating theorems. To fully appreciate and understand their beauty and to help study for GCSE maths, it is vital to conduct further research and explore mathematical theorems and proofs. Here are some suggested resources to deepen your understanding:

BBC Bitesize – has various resources, quizzes and videos for GCSE maths, including theorems.
Maths Genie – offers a wide range of free resources, including revision guides, exam questions and solutions. You can find detailed explanations and practice problems for various theorems.
Online Learning College GCSE Maths Hub – we have various blogs and resources on many GCSE maths topics, including theorems.
Tes GCSE maths revision resources – features a variety of challenging and engaging revision resources designed by educators to help students prepare for exams. Some cost, but others are free.
Textbooks – there are many textbooks from exam boards, CGP and Cambridge University Press on GCSE maths.

Don’t forget your exam board, as they will have various resources, and there may also be various YouTube videos that could be useful